DBSCANクラスタリングの解説と実験

前回の記事は密度ベースクラスタリングのOPTICSクラスタリングを解説しました。

今回の記事はもう一つの密度ベースクラスタリングのDBSCANクラスタリングを解説と実験します。

DBSCANとは

DBSCAN (Density-based spatial clustering of applications with noise ) は、1996 年に Martin Ester, Hans-Peter Kriegel, Jörg Sander および Xiaowei Xu によって提案された密度準拠クラスタリングのアルゴリズムです。半径以内に点がいくつあるかでその領域をクラスタとして判断します。近傍の密度がある閾値を超えている限り，クラスタを成長させ続けます。半径以内に近く点がない点はノイズになります。

長所

１）k-meansと違って，最初にクラスタ数を決めなくてもクラスターを作成できます。
２）とがったクラスターでも分類できます。クラスターが球状であることを前提としない。
３）近傍の密度でクラスターを判断します。

短所

１）border点の概念が微妙で，データによりどのクラスタに属するか変わる可能性があります。
２）データがわからないとパラメータを決めるのが難しいです。

DBSCANの計算プロセスの例１

DBSCANのアルゴリズムは半径以内に確認します。半径以内に３個以上の点があれば、グループを成長させ続けます。左の2列は２点しかないなので、グループに属しません。また、一番下の行は半径以外なので、グループに属しません。

DBSCANの計算プロセスの例２

以上の例と同じ、DBSCANは半径以内に確認して、グループに属するかどうか判断します。最初は上からと下からでグループを確認します。上の確認は半径以外になると、途中に止まりました。このようにDBSCANのアルゴリズムはすべての点はグループを確認します。

DBSCANの論文：

A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise (University of Munic)

https://www.aaai.org/Papers/KDD/1996/KDD96-037.pdf

２．Sci-kit LearnのDBSCAN

sklearn.cluster.DBSCAN(eps=0.5, min_samples=5, metric=’euclidean’, metric_params=None, algorithm=’auto’, leaf_size=30, p=None, n_jobs=None)[source]

eps : float, optional：半径の距離
min_samples : int, optional：近傍の密度がある閾値
algorithm ：‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’のアルゴリズムを設定できます。
leaf_size : int, optional (default = 30)：BallTree or cKDTreeの葉のサイズ
p : float, optional：Minkowskiのメトリックの設定
n_jobs : int or None, optional (default=None)：実行する平行ジョブの数

３．コード・実験　(K-Mean++ vs DBSCAN)

概要：
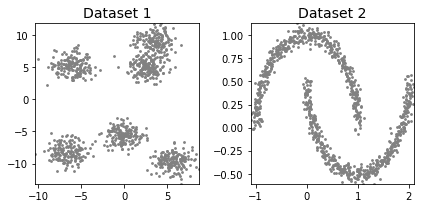
データセット：make_blobsとmake_moonsで塊と月の分類データセットを生成しました。
環境：google colab Python3 GPU
ライブラリ：　Sklearn
モデル：
実験1：k-mean++クラスタリング
実験2 ：DBSCANのクラスタリング
比較：クラスタの結果と実行時間

データセット生成

# ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import time
from sklearn.metrics import silhouette_score
from sklearn import cluster, datasets, mixture
from sklearn.neighbors import kneighbors_graph

# 塊のデータセット
dataset1 = datasets.make_blobs(n_samples=1000, random_state=10, centers=6, cluster_std=1.2)[0]

# 月のデータセット
dataset2 = datasets.make_moons(n_samples=1000, noise=.05)[0]

# グラフ作成
def cluster_plots(set1, set2, colours1 = 'gray', colours2 = 'gray', title1 = 'Dataset 1', title2 = 'Dataset 2'):

fig,(ax1,ax2) = plt.subplots(1, 2)
fig.set_size_inches(6, 3)

ax1.set_title(title1,fontsize=14)
ax1.set_xlim(min(set1[:,0]), max(set1[:,0]))
ax1.set_ylim(min(set1[:,1]), max(set1[:,1]))
ax1.scatter(set1[:, 0], set1[:, 1],s=8,lw=0,c= colours1)

ax2.set_title(title2,fontsize=14)
ax2.set_xlim(min(set2[:,0]), max(set2[:,0]))
ax2.set_ylim(min(set2[:,1]), max(set2[:,1]))
ax2.scatter(set2[:, 0], set2[:, 1],s=8,lw=0,c=colours2)

fig.tight_layout()
plt.show()

cluster_plots(dataset1, dataset2)

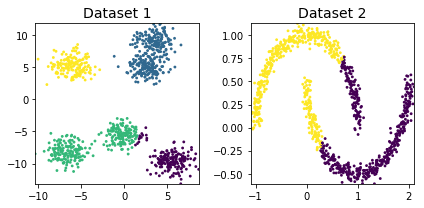
k-mean++クラスタリング

# k-mean++クラスタリング
start_time = time.time()

kmeans_dataset1 = cluster.KMeans(n_clusters=4, max_iter=300, init='k-means++',n_init=10).fit_predict(dataset1)
kmeans_dataset2 = cluster.KMeans(n_clusters=2, max_iter=300, init='k-means++',n_init=10).fit_predict(dataset2)
print("--- %s seconds ---" % (time.time() - start_time))
print('Dataset1')
print(*["Cluster "+str(i)+": "+ str(sum(kmeans_dataset1==i)) for i in range(4)], sep='\n')
cluster_plots(dataset1, dataset2, kmeans_dataset1, kmeans_dataset2)

— 0.06035923957824707 seconds —
Dataset1
Cluster 0: 180
Cluster 1: 333
Cluster 2: 320
Cluster 3: 167

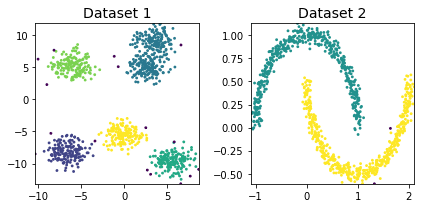
DBSCANクラスタリング

# DBSCANクラスタリングを作成
start_time = time.time()

dbscan_dataset1 = cluster.DBSCAN(eps=1, min_samples=5, metric='euclidean').fit_predict(dataset1)
dbscan_dataset2 = cluster.DBSCAN(eps=1, min_samples=5, metric='euclidean').fit_predict(dataset2)

# noise points are assigned -1
print("--- %s seconds ---" % (time.time() - start_time))
print('Dataset1:')
print("Number of Noise Points: ",sum(dbscan_dataset1==-1)," (",len(dbscan_dataset1),")",sep='')
print('Dataset2:')
print("Number of Noise Points: ",sum(dbscan_dataset2==-1)," (",len(dbscan_dataset2),")",sep='')
dbscan_dataset2 = cluster.DBSCAN(eps=0.1, min_samples=5, metric='euclidean').fit_predict(dataset2)
cluster_plots(dataset1, dataset2, dbscan_dataset1, dbscan_dataset2)

— 0.03548407554626465 seconds —
Dataset1:
Number of Noise Points: 16 (1000)
Dataset2:
Number of Noise Points: 0 (1000)

４．まとめ

DBSCANクラスタリングを解説と実験しました。二次元のデータセットにたいしてk-meanにより、DBSCANがうまく分類できます。また、ノイズも判断できます。最後に、k-meansより、DBSCANの実行時間が二倍くらい早いです。（DBSCAN＝0.35 k-mean=0.60 　）

参考：scikit-learn
https://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html

参照：クラスタリングの可視化
https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

目次：