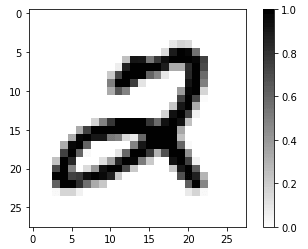目次
1. AdaDelta最適化アルゴリズムの概要
1.1 AdaDelta最適化アルゴリズムとは
1.2 AdaDelta関数
2. 実験
2.1 ライブラリインポート
2.2 データ読み込み
2.3 データ加工
2.4 AdaDeltaの最適化アルゴリズムを作成
2.3 Adamの最適化アルゴリズムを作成
2.5 まとめ
1. AdaDelta最適化アルゴリズムの概要
1.1 AdaDelta最適化アルゴリズムとは
AdadeltaはAdagradの拡張版の最適化アルゴリズムです。 過去のすべての勾配を累積するのではなく、勾配更新の固定移動ウィンドウに基づいて、単調に減少する学習率を下げていくような最適化アルゴリズムです。複数の値を保持するのではないのでAdagradに比べるとメモリー効率も良いと言われています。
ADAGRADメソッドでは、分母はトレーニングの開始から始まる各反復からの二乗勾配を累積します。 各項が正であるため、この累積合計はトレーニング全体を通じて増加し続け、各次元の学習率を効果的に縮小します。 何度もイテレーションの繰り返した後、学習率は非常に小さくなります。
下記の計算式になります。注意点としてはステップ5で差分を取っています。これは、無次元かと呼ばれる操作で学習していきます。この無次元かと呼ばれる特徴を用いているため、他のステップでも学習率を設定しないアルゴリズムです。
論文:ADADELTA: An Adaptive Learning Rate Method
https://arxiv.org/abs/1212.5701
1.2 AdaDelta関数
Tensorflow
tf.keras.optimizers.Adadelta(
learning_rate=0.001, rho=0.95, epsilon=1e-07, name=’Adadelta’,
**kwargs
)
https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/Adadelta
Pytorch
torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
detail:
https://pytorch.org/docs/stable/optim.html
2. 実験
データセット:digit MNIST 60,000枚の28×28,10個の数字の白黒画像と10,000枚のテスト用画像データセット。
モデル:AdaDeltaの最適化アルゴリズムのモデル vs Adamの最適化アルゴリズムのモデル
モデル評価:Accuracy
2.1 ライブラリインポート
| import os import sys import tensorflow as tf import tensorflow_datasets as tfds import math import numpy as np import logging from datetime import datetime import matplotlib.pyplot as plt
tfds.disable_progress_bar() |
2.2 データ読み込み
Tensorflowのデータセットを読み込みます。
| dataset, metadata = tfds.load(‘mnist’, as_supervised=True, with_info=True) train_dataset, test_dataset = dataset[‘train’], dataset[‘test’] |
クラス名を作成します。
| class_names = [‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’] |
2.3 データ加工
学習とテストのデータを分けます。
| num_train_examples = metadata.splits[‘train’].num_examples num_test_examples = metadata.splits[‘test’].num_examples print(“Number of training examples: {}”.format(num_train_examples)) print(“Number of test examples: {}”.format(num_test_examples)) |
Number of training examples: 60000
Number of test examples: 10000
データを正規化します。
| def normalize(images, labels): images = tf.cast(images, tf.float32) images /= 255 return images, labels
# Normalize train_dataset = train_dataset.map(normalize) test_dataset = test_dataset.map(normalize)
# Caching train_dataset = train_dataset.cache() test_dataset = test_dataset.cache() |
画像データを確認します。
| # Take a single image, and remove the color dimension by reshaping for image, label in test_dataset.take(1): break image = image.numpy().reshape((28, 28))
# Plot the image – voila a piece of fashion clothing plt.figure() plt.imshow(image, cmap=plt.cm.binary) plt.colorbar() plt.grid(False) plt.show() |
2.4 AdaDeltaの最適化アルゴリズムを作成
| # Create Model model = tf.keras.Sequential([ tf.keras.layers.Flatten(input_shape=(28, 28)), tf.keras.layers.Dense(128, activation=tf.nn.relu), tf.keras.layers.Dense(10, activation=tf.nn.softmax) ])
model.compile(optimizer=’AdaDelta’, loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics=[‘accuracy’])
BATCH_SIZE = 128 EPOCHS = 50 train_dataset = train_dataset.cache().repeat().shuffle(num_train_examples).batch(BATCH_SIZE) test_dataset = test_dataset.cache().batch(EPOCHS)
history = model.fit(train_dataset, epochs=EPOCHS, steps_per_epoch=math.ceil(num_train_examples/BATCH_SIZE)) |
Epoch 1/50
469/469 [==============================] – 7s 4ms/step – loss: 2.2896 – accuracy: 0.1312
…
Epoch 50/50
469/469 [==============================] – 2s 4ms/step – loss: 0.6264 – accuracy: 0.8586
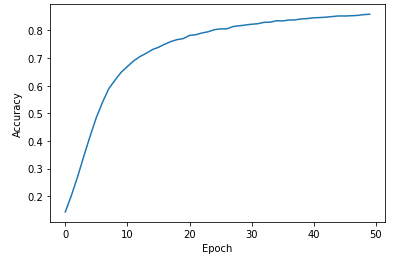
モデル評価
| # Plot loss plt.xlabel(‘Epoch’) plt.ylabel(‘Accuracy’) plt.plot(history.history[‘accuracy’])
test_loss, test_accuracy = model.evaluate(test_dataset, steps=math.ceil(num_test_examples/32)) print(‘Accuracy on test dataset:’, test_accuracy |
Accuracy on test dataset: 0.8652999997138977
2.3 Adamの最適化アルゴリズムを作成
| # Create Model model = tf.keras.Sequential([ tf.keras.layers.Flatten(input_shape=(28, 28)), tf.keras.layers.Dense(128, activation=tf.nn.relu), tf.keras.layers.Dense(10, activation=tf.nn.softmax) ])
model.compile(optimizer=’adam’, loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics=[‘accuracy’])
BATCH_SIZE = 128 EPOCHS = 50 train_dataset = train_dataset.cache().repeat().shuffle(num_train_examples).batch(BATCH_SIZE) test_dataset = test_dataset.cache().batch(EPOCHS)
history = model.fit(train_dataset, epochs=EPOCHS, steps_per_epoch=math.ceil(num_train_examples/BATCH_SIZE)) |
Epoch 1/50
469/469 [==============================] – 7s 4ms/step – loss: 0.6344 – accuracy: 0.8256
…
Epoch 50/50
469/469 [==============================] – 2s 4ms/step – loss: 1.8086e-04 – accuracy: 1.0000
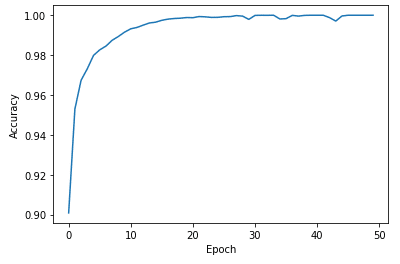
| # Plot loss plt.xlabel(‘Epoch’) plt.ylabel(‘Accuracy’) plt.plot(history.history[‘accuracy’])
test_loss, test_accuracy = model.evaluate(test_dataset, steps=math.ceil(num_test_examples/32)) print(‘Accuracy on test dataset:’, test_accuracy)
|
Accuracy on test dataset: 0.9811000227928162
2.5 まとめ
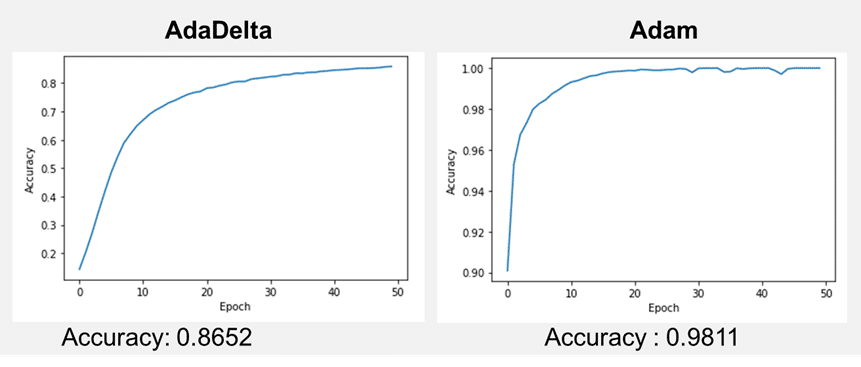
MNISTの手書き数字データセットで、AdaDeltaの最適化アルゴリズムのモデル と Adamの最適化アルゴリズムのモデルを作成しました。どちらもよく学習しましたが、AdaDeltaの方が学習遅いと考えられます。理由としては、学習率を非常に小さくしていくからだと思います。もっと、Epochを増やさないと、アンダーフィットの状態かつ学習がまだまだ必要である事がわかりました。
担当者:HM
香川県高松市出身 データ分析にて、博士(理学)を取得後、自動車メーカー会社にてデータ分析に関わる。その後コンサルティングファームでデータ分析プロジェクトを歴任後独立 気が付けばデータ分析プロジェクトだけで50以上担当
理化学研究所にて研究員を拝命中 応用数理学会所属