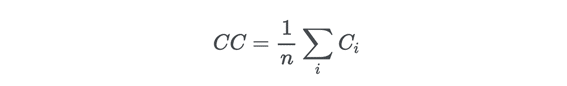目次
1. Networkxのクラスタリング(コミュニティ)
1.1 コミュニティとは
1.2 ガーバンニューマンのアルゴリズム
1.3 クラスタリング係数
2. 実験
2.1 環境準備
2.2 データ準備
2.3 ガーバンニューマンのアルゴリズム
2.4 クラスタリング係数
1. Networkxのクラスタリング(コミュニティ)
1.1 コミュニティとは
コミュニティは、接続されたノードの集まりです。 コミュニティ内のノードは密に接続されていますが、中でのクラスタリング結果されたものを指します。
1.2 ガーバンニューマンのアルゴリズム
コミュニティを見つけるアルゴリズムの中に、ガーバンニューマン(GirvanNewma) アルゴリズムというものがあります。 ネットワーク内のエッジを段階的に削除することにより、コミュニティを識別します。 中間性を「エッジ中間性」と呼びます。 これは、このエッジを通過するノードのペア間の最短パスの数に比例するスコアです。
このアルゴリズムの手順は次のとおりです。
- ネットワーク内の既存のすべてのエッジの中間性を計算します。
- 中間が最も高いエッジを削除します。
- このエッジを削除した後、すべてのエッジの間隔を再計算します。
- エッジがなくなるまで、手順2と3を繰り返します。
1.3 クラスタリング係数
ローカルクラスタリング係数は、ノードiを中心とする三角形の数とノードiを中心とする三角形の数の比率です。 ある意味で、ノードiとその隣接ノードが完全グラフにどれだけ近いかを測定します。
実際の例としては、ノードαがノードβとノードγのどちらにも繋がっており、さらにノードβとノードγに繋がっている時だと三角形αβγが形成されています。このような三角形を多く含むネットワークは「クラスターの密度が高い」と考えていくのがこのローカルクラスタリングの考え方です。
これを全体として求めるのがグローバル係数であり、グラフ内の三角形(ローカルクラスター)の密度を測定します。
2. 実験
環境:Google Colab (networkxのパッケージがインストールしている)
データセット:networkxのFlorentine Families:結婚の絆によって、ルネッサンスのフィレンツェの家族間の同盟を描いたフィレンツェの家族のグラフです。
モデル:ガーバンニューマンのアルゴリズム
2.1 環境準備
ライブラリのインポート
| %matplotlib inline import numpy as np import networkx as nx import matplotlib.pyplot as plt |
2.2 データ準備
Florentine Familiesのデータをロードします。
| G = nx.florentine_families_graph()
print(nx.info(G)) print(G.nodes)
nx.draw(G, node_color=’skyblue’, edge_color=’lightblue’, with_labels=True) |
Name:
Type: Graph
Number of nodes: 15
Number of edges: 20
Average degree: 2.6667
[‘Acciaiuoli’, ‘Medici’, ‘Castellani’, ‘Peruzzi’, ‘Strozzi’, ‘Barbadori’, ‘Ridolfi’, ‘Tornabuoni’, ‘Albizzi’, ‘Salviati’, ‘Pazzi’, ‘Bischeri’, ‘Guadagni’, ‘Ginori’, ‘Lamberteschi’]
2.3 ガーバンニューマンのアルゴリズム
ガーバンニューマンのアルゴリズムを計算します。3つのコンミュニティを分けます。
| from networkx.algorithms import community import itertools
k = 3 comp = community.girvan_newman(G) community_list = []
for communities in itertools.islice(comp, k-1): community_list.append(tuple(sorted(c) for c in communities))
community_list = list(community_list[k-2]) community_list
|
[[‘Acciaiuoli’,
‘Albizzi’,
‘Ginori’,
‘Guadagni’,
‘Lamberteschi’,
‘Medici’,
‘Ridolfi’,
‘Tornabuoni’],
[‘Barbadori’, ‘Bischeri’, ‘Castellani’, ‘Peruzzi’, ‘Strozzi’],
[‘Pazzi’, ‘Salviati’]]
コンミュニティのグラフを作成します。
| # Color node
color_map = [] for node in G: if node in community_list[0]: color_map.append(‘silver’) elif node in community_list[1]: color_map.append(‘yellow’) else: color_map.append(‘skyblue’) nx.draw(G, node_color=color_map, with_labels=True)
|
2.4 クラスタリング係数
ローカルクラスタリング係数を計算します。
| # Clustering Coefficient nx.clustering(G) |
{‘Acciaiuoli’: 0,
‘Albizzi’: 0,
‘Barbadori’: 0,
‘Bischeri’: 0.3333333333333333,
‘Castellani’: 0.3333333333333333,
‘Ginori’: 0,
‘Guadagni’: 0,
‘Lamberteschi’: 0,
‘Medici’: 0.06666666666666667,
‘Pazzi’: 0,
‘Peruzzi’: 0.6666666666666666,
‘Ridolfi’: 0.3333333333333333,
‘Salviati’: 0,
‘Strozzi’: 0.3333333333333333,
‘Tornabuoni’: 0.3333333333333333}
グローバルクラスタリング係数を計算します。
| # Global clustering coefficient np.mean(list(nx.clustering(G).values())) |
0.16
担当者:HM
香川県高松市出身 データ分析にて、博士(理学)を取得後、自動車メーカー会社にてデータ分析に関わる。その後コンサルティングファームでデータ分析プロジェクトを歴任後独立 気が付けばデータ分析プロジェクトだけで50以上担当
理化学研究所にて研究員を拝命中 応用数理学会所属