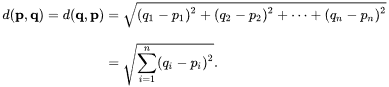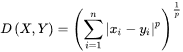目次
1. 距離 とは
2. ユークリッド距離 (euclidean distance)
3. マンハッタン距離 (manhattan distance)
4. ミンコフスキー距離 (Minkowski distance)
5. チェビシェフ距離(Chebyshev distance)
6. ハミング距離(Hamming distance)
1. 距離 とは
距離 とは2つのデータが似ている度合いを,類似度の大きさや距離の近さといった数値にしてあらわすことです。機械学習では、多くの機械学習タスクで使用されるデータの類似性と距離を測定します。クラスター分析、レコメンダシステム、自然言語処理(NLP)に色々な距離アルゴリズムが必要です。今回の記事は下記の距離と類似度を解説します。
・ ユークリッド距離 (euclidean distance)
・ マンハッタン距離 (manhattan distance)
・ ミンコフスキー距離 (Minkowski distance)
・ チェビシェフ距離(Chebyshev distance)
・ ハミング距離(Hamming distance)
2. ユークリッド距離 (英:euclidean distance)
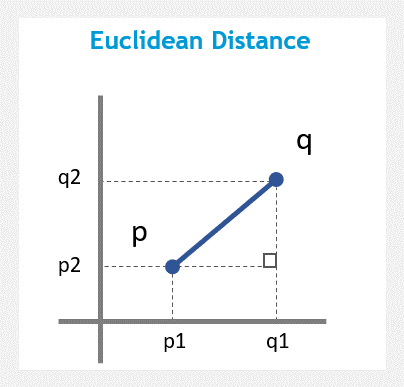
ユークリッド距離は、2つのベクトル間の直線距離です。点pとqの間のユークリッド距離は、それらを結ぶ線分の長さです。高次元でマンハッタン距離やチェビシェフ距離よりノイズに強いので、距離差が出にくいです。
計算式:
Python script:
import scipy.spatial.distance as dist
A = [(1, 1)]
B = [(4, 5)]
euclidean_distance = dist.euclidean(A, B)
print("Euclidean distance is {:.4f}".format(euclidean_distance))Euclidean distance is 5.0000
3. マンハッタン距離 (英:manhattan distance)
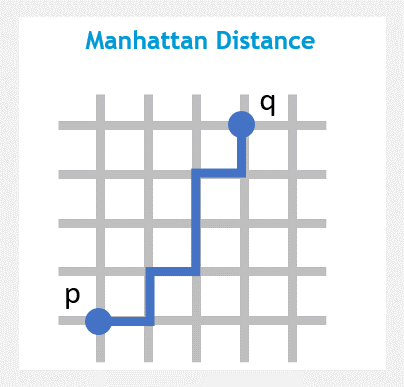
マンハッタン距離(またはタクシーメトリック)は、グリッド上のポイント間の水平距離と垂直距離の合計です。マンハッタン距離の名は、マンハッタンのような正方形のブロックに区分された都市で、自動車が運転される距離に由来します。外れ値がある場合は、マンハッタン距離はエラーを削減しようとします。
計算式:
Python Script:
import scipy.spatial.distance as dist
A = [(1, 1)]
B = [(4, 5)]
manhattan_distance = dist.cityblock(A, B)
print("Manhattan distance is {:.4f}".format(manhattan_distance))Manhattan distance is 7.0000
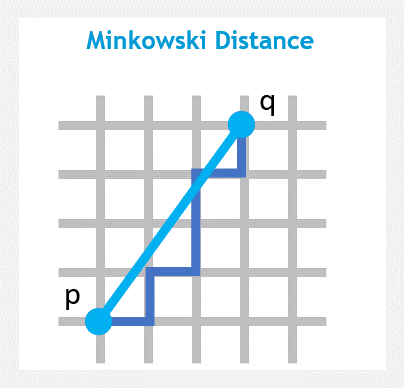
4. ミンコフスキー距離 (英:Minkowski distance)
ミンコフスキー距離は、ユークリッド距離とマンハッタン距離の一般化する距離アルゴリズムです。n次元のベクトル x1 と x2 の距離関数が次式で表される距離。p=2ならEuclid距離で,p=1ならManhattan距離,p=∞ならChebyshev距離です。
計算式:
Python Script:
import scipy.spatial.distance as dist
A = [(1, 1)]
B = [(4, 5)]
minkowskin_distance = dist.minkowski(A, B, w=(0.5,1.5))
# w = The weights for each value in A and B.
print("Minkowski distance is {:.4f}".format(minkowskin_distance))Minkowski distance is 5.3385
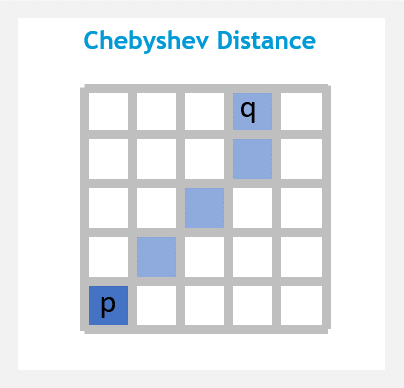
5. チェビシェフ距離(英:Chebyshev distance)
チェビシェフ距離(またはチェビシェフ距離、最大距離、チェス盤距離)は、2つのN次元点の1次元における最大絶対距離である距離です。 チェス、倉庫物流、倉庫のチェビシェフ距離にクレーンの移動、その他多くの分野で実際の用途があります。
計算式:
Python Script:
import scipy.spatial.distance as dist
A = [(1, 1)]
B = [(4, 5)]
chebyshev_distance = dist.chebyshev(A, B)
print("Chebyshev distance is {:.4f}".format(chebyshev_distance))Chebyshev distance is 4.0000
6. ハミング距離(Hamming distance)
ハミング距離は、2つのバイナリデータ文字列を比較するためのメトリックです。 同じ長さの2つのバイナリ文字列を比較する場合、ハミング距離は2つのビットが異なるビット位置の数です。データがコンピュータネットワークを介して送信されるときのエラー検出またはエラー修正に使用されます。 また、同じ長さのデータワードを比較するためのコーディング理論でも使用されています。
ハミング距離の計算の例:
1110000 と 1110011 の間のハミング距離は 2 である。
distance と distancr の間のハミング距離は 1 である。
Python Script
import scipy.spatial.distance as dist
A = [(110, 100)]
B = [(110, 110)]
hamming_distance = dist.hamming(A, B)
print("Hamming distance is {:.4f}".format(hamming_distance))Hamming distance is 0.5000