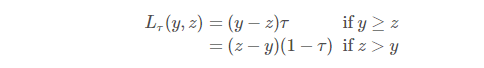ピンボールロス（Pinball loss）の解説

目次

1. ピンボールロス（Pinball loss）の概要
＿＿1.1ピンボールロス（Pinball loss）とは
＿＿1.2ピンボールロスのロジック

2. 実験・コード
＿＿2.1 環境の準備
＿＿2.2 データロード
＿＿2.3 モデル・結果作成
＿＿2.4可視化・評価

3. まとめ

1. ピンボールロス（Pinball loss）の概要

1.1 ピンボールロス（Pinball loss）とは　分位点ロス（quantile loss）

ピンボールロス関数または分位点ロス（quantile loss）、分位予測の学習する時に、使用される損失関数です。分位回帰は、偏りに強い回帰の種類になります。 予測される変数の平均を求める代わりに、分位点回帰では中央値と他の分位点を求めます。

τをターゲット分位数、yを実際の値、zを分位数予測とすると、ピンボール損失関数であるLτは次のように記述できます。

1.2ピンボールロスのロジック

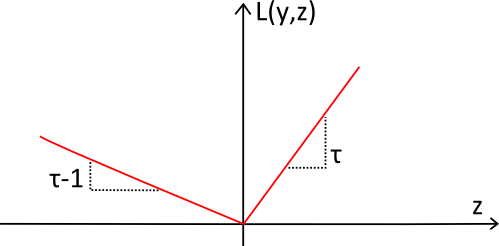
「下記の図」ピンボールロス関数（赤）は、ピンボール上のボールの軌道の形状にちなんで名付けられました。 関数は常に正であり、ターゲットyから離れるほど、Lτ（y、z）の値は大きくなります。 傾斜は、分位数予測における望ましい不均衡を反映するために使用されます。

観測値から可能な限り近い予測を目標とする従来の予測とは異なり、分位点を予測するのに適した損失関数です。

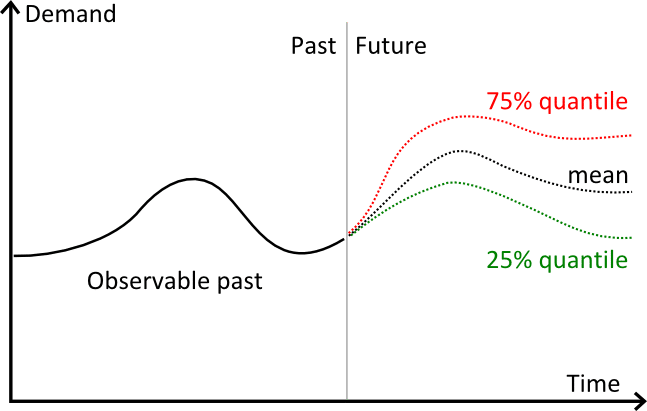
上のグラフは、3つの異なる予測を示しています。
赤字は75％の分位数予測
黒字、平均の予測
緑色で、25％分位数予測

2. 実験・コード

環境：Google Colab
データセット：scikit-learnのBoston house-prices (ボストン市の住宅価格)
モデル：１）線形回帰（LinearRegression）
２）勾配ブースティング（Gradient Boosting）
３）分位点回帰（Quantile Regression）
モデル評価：ピンボールロス（Pinball loss）

2.1 環境の準備

ライブラリのインポート

import numpy as np
import pandas as pd
from statistics import mean

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression
from sklearn.ensemble import GradientBoostingRegressor
import statsmodels.api as sm
import statsmodels.formula.api as smf

import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, r2_score

SEED=0

ピンボールロス関数作成

def pinball_loss(q, y, f):
# q: 分位数 y: 実績値 f: 予測値
e = y - f
return np.maximum(q * e, (q - 1) * e)

2.2 サンプルデータ作成

X, y = make_regression(n_targets=1, n_features=1, n_samples=270, noise=60 , random_state=0)

異常データを追加

y[0] = y[0]+50000
y[1] = y[1]+50000
y[2] = y[2]+50000
y[3] = y[3]+50000
y[4] = y[4]+50000

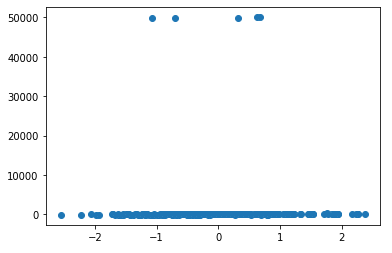
分布図を可視化

plt.scatter(X, y)

学習データと検証データを分けます。

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
print(len(X_train))
print(len(X_test))

202
68

2.3 線形回帰（Linear Regression）

モデル作成

lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred = lr.predict(X_test)

モデル評価

lr_MSE = mean_squared_error(y_test, y_pred)
lr_R2 = r2_score(y_test, y_pred)
lr_PBL = mean(pinball_loss(0.5, y_test, y_pred))

print("LinearRegression MSE:", lr_MSE)
print("LinearRegression R2:", lr_R2)
print("LinearRegression Pinball Loss:", lr_PBL)

LinearRegression MSE: 1522275.2781386205
LinearRegression R2: -221.85133685906928
LinearRegression Pinball Loss: 615.9531099002489

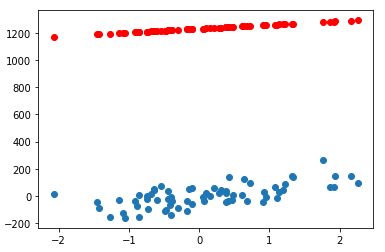
分布図を可視化

plt.scatter(X_test, y_test)
plt.plot(X_test, y_pred, 'or')
plt.show()

2.4勾配ブースティング（Gradient Boosting）

モデル作成

gbr = GradientBoostingRegressor(loss='quantile', random_state=SEED)
gbr.fit(X_train, y_train)
y_pred = gbr.predict(X_test)

3. モデル評価

gbr_MSE = mean_squared_error(y_test, y_pred)
gbr_R2 = r2_score(y_test, y_pred)
gbr_PBL = mean(pinball_loss(0.5, y_test, y_pred))

print("GradientBoostingRegressor MSE:", gbr_MSE)
print("GradientBoostingRegressor R2:", gbr_R2)
print("GradientBoostingRegressor Pinball Loss:", gbr_PBL)

GradientBoostingRegressor MSE: 3508337.5542622623
GradientBoostingRegressor R2: -512.598115497365
GradientBoostingRegressor Pinball Loss: 214.916416362088

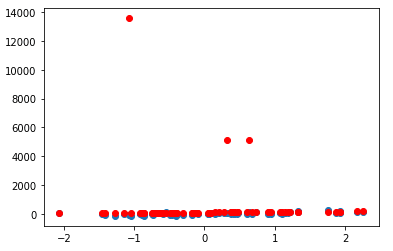
分布図

plt.scatter(X_test, y_test)
plt.plot(X_test, y_pred, 'or')
plt.show()

2.5 分位点回帰（Quantile Regression）

データ加工

X_train_f = [item for sublist in X_train for item in sublist]
X_test_f = [item for sublist in X_test for item in sublist]
data_tuples = list(zip(y_train, X_train_f))
train_df = pd.DataFrame(data_tuples, columns=['y','X'])
test_df = pd.DataFrame(X_test_f, columns=['y'])

モデル作成

mod = smf.quantreg('X ~ y', train_df)
qtr = mod.fit(q=.5)
y_pred = qtr.predict(test_df)

モデル評価

qtr_MSE = mean_squared_error(y_test, y_pred)
qtr_R2 = r2_score(y_test, y_pred)
qtr_PBL = mean(pinball_loss(0.5, y_test, y_pred))

print("QuantileRegressor MSE:", qtr_MSE)
print("QuantileRegressor R2:", qtr_R2)
print("QuantileRegressor Pinball Loss:", qtr_PBL)

QuantileRegressor MSE: 6837.715009306304
QuantileRegressor R2: -0.000997620317706005
QuantileRegressor Pinball Loss: 32.29794183320969

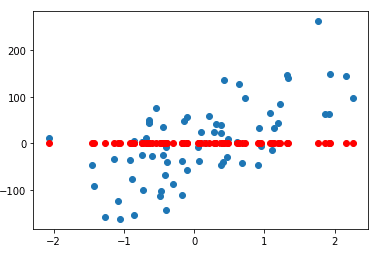
分布図

plt.scatter(X_test, y_test)
plt.plot(X_test, y_pred, 'or')
plt.show()

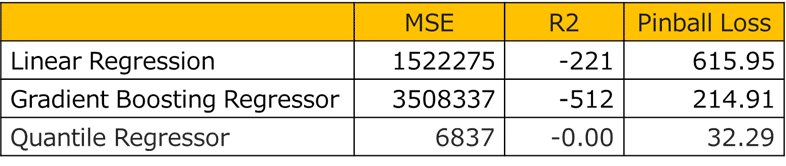
まとめ

本稿ではピンボールロスの概要や仕組み、非常値あるデータセットを利用して 線形回帰（Linear　Regression）、勾配ブースティング（Gradient Boosting）、分位点回帰（Quantile Regressionのモデルを作成致しました。MSE, R2 ピンボールロスの検査を見ると、分位点回帰は一番良い結果になっています。外れ値に強いのが特徴です。