前回の記事は複数のクラスタリングのシリーズを説明しました。この記事では、回帰分析のお話になります。
では、線形回帰から始めましょう。線形回帰は、最も基本的なモデルです。しかし拡張してより複雑なデータ動作をモデル化することができます。
線形回帰とは
線形回帰とは、一般的に使用される予測分析方法です。目的変数 と 1 以上の説明変数の間の線形関係を使用して、目的変数を予測する分析です。例えば、過去の価格と売上増加の関係を分析して将来の価格戦略を決定できます。
では、Pythonで線形回帰実験しましょう。
標準的なインポートから始めます。
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
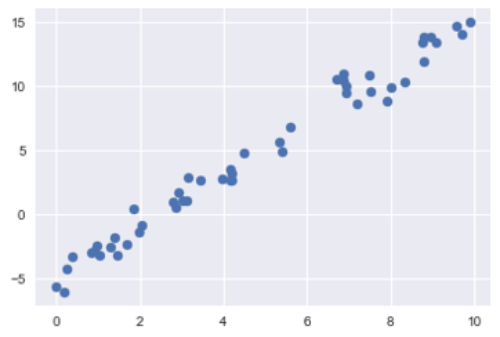
次は50件のサンプルデータを作成して、散布図を描きます。
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = 2 * x - 5 + rng.randn(50)
plt.scatter(x, y);
Scikit-Learn’s のLinearRegressionを利用し、線形回帰を作成します。
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model.fit(x[:, np.newaxis], y)
xfit = np.linspace(0, 10, 1000)
yfit = model.predict(xfit[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit);
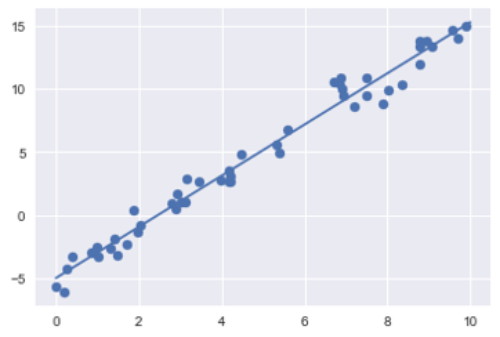
一変数の関係では、線形回帰は y = ax+bという方程式で表します。
yが予測したい目的変数、xが予測に使える説明変数です。
a を傾き、b を切片と言います。傾きは直線の勾配を示し、切片は軸との交差位置を示します。
では、勾配と切片を計算しましょう。
print("Model slope: ", model.coef_[0])
print("Model intercept:", model.intercept_)
結果:
Model slope: 2.02720881036
Model intercept: -4.99857708555
より複雑なモデルにしようとしたとき、最初は変数を増やしていく事になります。
y=a0+a1x1+a2x2+⋯
全く単純な手続きですが、たったこれだけで曲線を使った回帰ができるようになります。
これが(n次)多項式回帰と呼ばれるモデルです。
では、多次元線形のサンプルデータを作成しましょう。
rng = np.random.RandomState(1)
X = 10 * rng.rand(100, 3)
y = 0.5 + np.dot(X, [1.5, -2., 1.])
model.fit(X, y)
from sklearn.preprocessing import PolynomialFeatures
x = np.array([2, 3, 4])
poly = PolynomialFeatures(3, include_bias=False)
poly.fit_transform(x[:, None])
多項式回帰のモデル作成
from sklearn.pipeline import make_pipeline
poly_model = make_pipeline(PolynomialFeatures(7),
LinearRegression())
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)
poly_model.fit(x[:, np.newaxis], y)
yfit = poly_model.predict(xfit[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit);
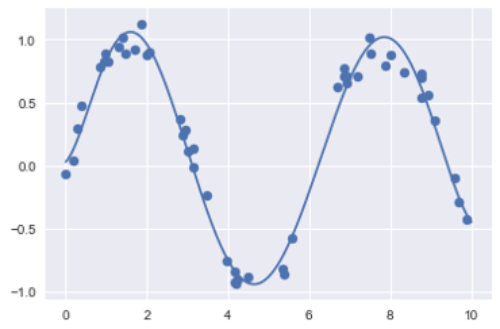
9次多項式を生成する関数でグラフの見た目から明らかに回帰が改善しています。
モデルが高度になるほどおかしな結果が出るとは納得がいかないことがあります、意味が無いではないか!これは機械学習で過学習(overfitting)と呼ばれる現象があります。これは次回以降また説明していきます。
詳細な情報は以下をご覧ください
https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.htmlS
https://ja.wikipedia.org/wiki/%E5%9B%9E%E5%B8%B0%E5%88%86%E6%9E%90

Pingback: Statsmodelsでの回帰分析 | S-Analysis