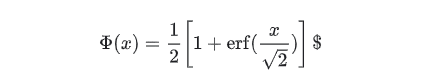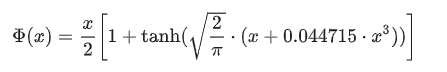目次
1 活性化関数とは
2. 活性化関数のまとめ
– ReLu関数
– Leaky ReLU関数
– PReLU関数
– ELU関数
– sigmoid関数
– TanH関数
– softmax 関数
– GELU関数
– SELU関数
-その他まとめ
1 活性化関数とは
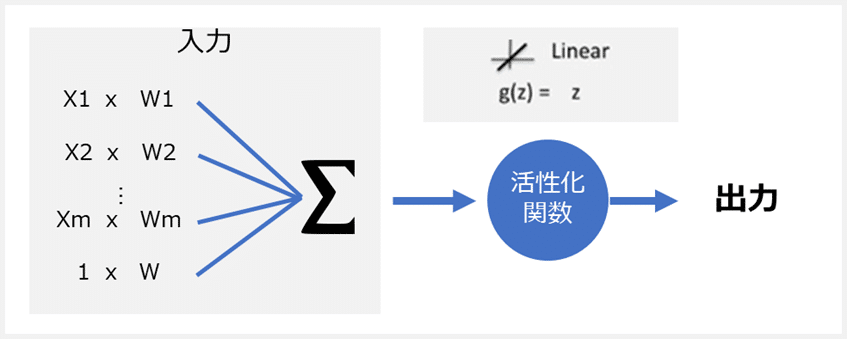
活性化関数は、(英: Activation functions)ニューラルネットワークの出力を決定する数式です。この関数はネットワーク内の各ニューロンに関連付けられており、各ニューロンの入力がアクティブ化(「起動」)するかどうかを決定します。各ニューロンの出力を1〜0または-1〜1の範囲に正規化するのにも役立ちます。
2. 活性化関数のまとめ
ReLu関数
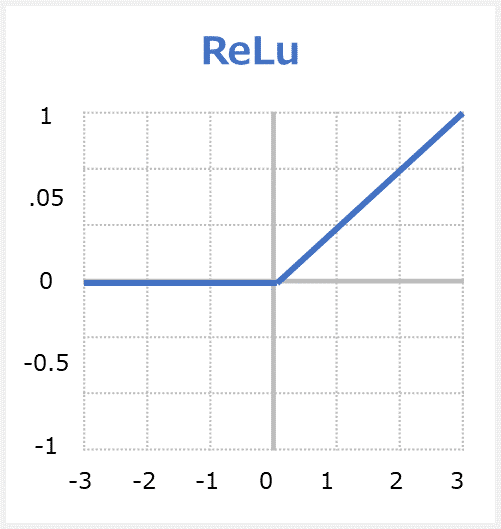
ReLu関数(「ランプ」と読む)はRectified Linear Unitの略称で、ランプ関数もと呼ばれています。関数への入力値が0以下の場合には出力値が常に0、入力値が0より上の場合には出力値が入力値と同じ値となる関数です。
ReLUのメリット
・非常に迅速に収束するネットワークなので、処理が速いです。
・勾配消失問題に強いです。勾配消失問題は層が深くなるにつれ勾配が消えてしまう。
・linear関数のように見えますが、ReLUには微分関数があり、バックプロパゲーションが可能です。
ReLUのデメリット
・入力がゼロに近づくか、負の場合、関数の勾配はゼロになり、ネットワークはバックプロパゲーションを実行できず、学習できません。
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/api_docs/python/tf/keras/activations/relu
PyTorch
https://pytorch.org/docs/stable/generated/torch.nn.ReLU.html
Leaky ReLU関数
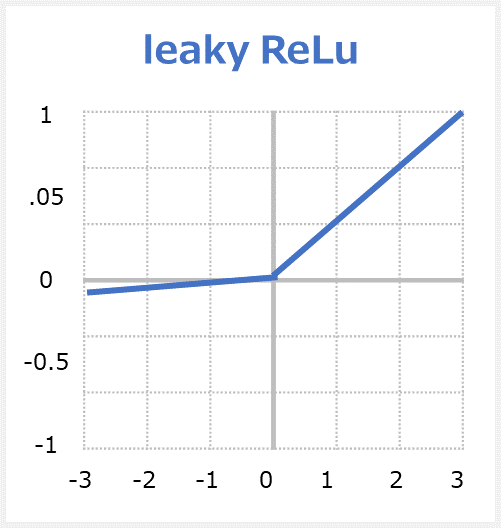
Leaky ReLU関数はLeaky Rectified Linear Unitの略称で、ReLUの拡張版です。関数への入力値が0より下の場合には出力値が入力値をα倍した値(※αの値は基本的に0.01)、入力値が0以上の場合には出力値が入力値と同じ値となる関数です。
Leaky ReLUのメリット
– Dying ReLUの問題が発生するのを防ぎます。ReLUのバリエーションは、負の領域に小さな正の傾きがあるため、負の入力値の場合でも逆伝播が可能になります。
・処理が速いです。
・勾配消失問題の解消します。
Leaky ReLUのデメリット
・結果に一貫性がない
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/api_docs/python/tf/nn/leaky_relu
PyTorch
https://pytorch.org/docs/stable/generated/torch.nn.LeakyReLU.html
論文
https://arxiv.org/pdf/1505.00853.pdf
PReLU関数
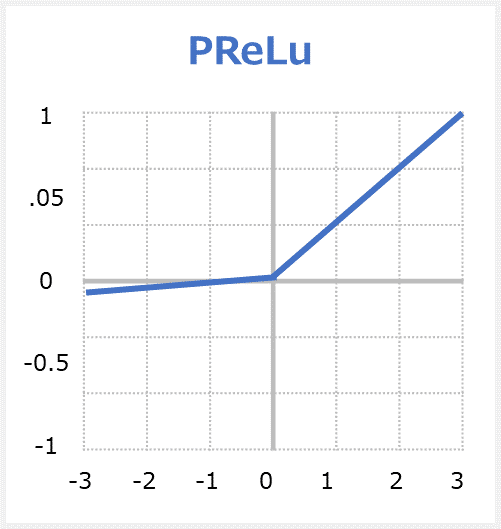
PReLU関数はParametric Rectified Linear Unitの略称で、Leaky ReLUの拡張版です。関数への入力値が0より下の場合には出力値が入力値をα倍した値(※αはパラメーターであり学習によって決まる)、入力値が0以上の場合には出力値が入力値と同じ値となる関数です。
Parametric ReLUでは「Parametric(パラメーターの)」という言葉の通り、学習によって動的に決まるパラメーター値である点が異なります。
PReLUのメリット
・負の勾配を学習できます。リークのあるReLUとは異なり、この関数は関数の負の部分の勾配を引数として提供します。 したがって、バックプロパゲーションを実行して、αの最も適切な値を学習することが可能です。
PReLUのデメリット
・問題ごとにパフォーマンスが異なる場合があります。
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/api_docs/python/tf/keras/layers/PReLU
PyTorch
https://pytorch.org/docs/stable/generated/torch.nn.PReLU.html
論文
https://arxiv.org/abs/1502.01852
過去記事
elu関数
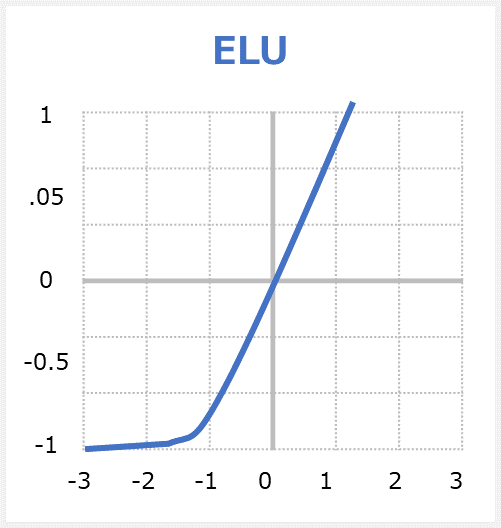
elu関数はExponential Linear Unitの略称でReLUの拡張版です。関数への入力値が0以下の場合には出力値が「0.0」~「-α」(※αの値は基本的に1.0、つまり「-1.0」)の間の値になり、入力値が0より上の場合には出力値が入力値と同じ値となる関数である。
eluのメリット
・Dying ReLUの問題はありません。
・この関数は、損失関数がより速くゼロに収束する傾向がある
・ReLUとLeakyReLUの優れた機能の統合の特徴
eluのデメリット
・大きな負の値ではサチュレイトゥになります。
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/api_docs/python/tf/keras/activations/elu
PyTorch
https://pytorch.org/docs/stable/generated/torch.nn.ELU.html
論文
https://arxiv.org/pdf/1511.07289.pdf
sigmoid関数
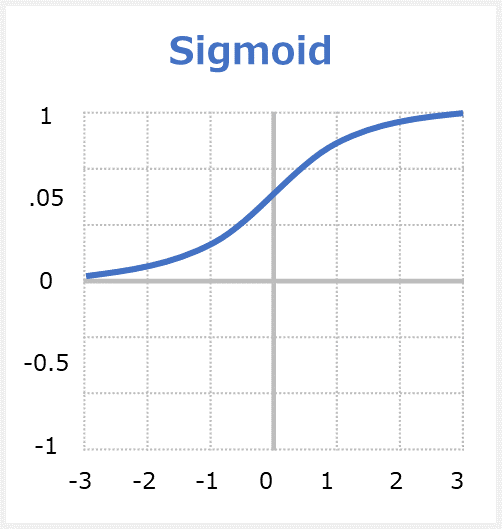
sigmoid関数(シグモイド)はStandard sigmoid functionの略称です。グラデーションで、0から1までの値を出力します。S(シグマ)字型曲線のグラフになるため、「シグモイド関数」と呼ばれます。
sigmoidのメリット
・滑らかなグラデーションで出力値の結論に飛び付くことを防ぎます。
・出力値は0と1の間にあり、各ニューロンの出力を正規化します。
・明確な予測-2より上または-2より下のXの場合、Y値(予測)が1または0に非常に近い曲線の端に来る傾向があります。これにより、明確な予測が可能になります。
sigmoidのデメリット
・Xの値が非常に高いか非常に低い場合、予測にほとんど変化がなく、勾配消失問題が発生します。 これにより、ネットワークがそれ以上の学習を拒否したり、速度が遅すぎて正確な予測に到達できなくなったりする可能性があります。
・ゼロ中心ではない出力
・大変な計算
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/api_docs/python/tf/keras/activations/sigmoid
PyTorch
https://pytorch.org/docs/stable/generated/torch.nn.Softmax.html
TanH関数
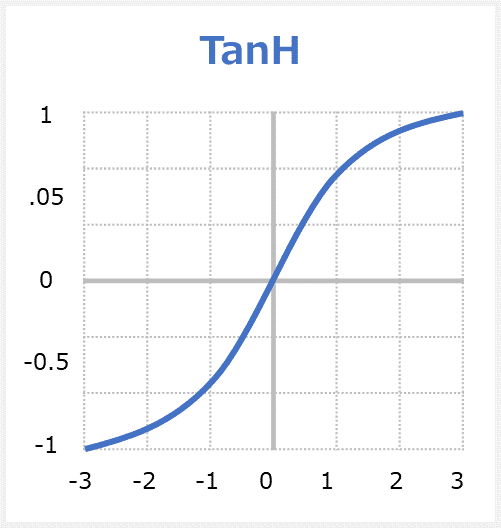
tanh関数(タンエイチ」はHyperbolic tangent functionの略称で、双曲線正接関数、「ハイパボリックタンジェント」です。あらゆる入力値を-1.0~1.0の範囲の数値に変換して出力する関数です。tanh関数は、シグモイド関数の拡張バージョンともいえる活性化関数である。
TanHのメリット
・ゼロ中心—強い負、中立、および強い正の値を持つ入力のモデル化が容易になります。
・滑らかなグラデーションで出力値の結論に飛び付くことを防ぎます。
・出力値は-1と1の間にあり、各ニューロンの出力を正規化します。
TanHのデメリット
・勾配消失問題の影響が強いです。
・大変な計算
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/api_docs/python/tf/keras/activations/tanh
PyTorch
https://pytorch.org/docs/stable/generated/torch.tanh.html
softmax 関数
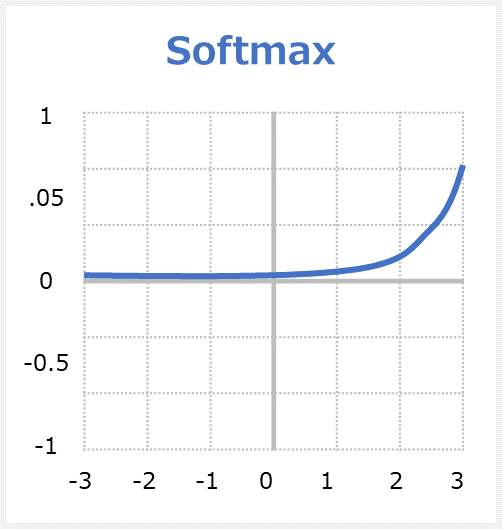
sigmoid関数(ソフトマックス)はsigmoid関数の拡張版の関数となっています。出力ニューロンに使用される特別な活性化関数。 各クラスの出力を0から1の間で正規化し、入力が特定のクラスに属する確率を返します。各出力値の範囲は0.0~1.0となります。滑らかな(=ソフトな)曲線となり、1つの出力値が最大となるため、「ソフトマックス関数」と呼ばれます。
softmaxのメリット
・他の活性化関数では1つのクラスのみで複数のクラスを処理できます。各クラスの出力を0から1の間で正規化し、それらの合計で除算して、入力値が特定のクラスにある確率を示します。
・出力ニューロンに役立ちます。通常、Softmaxは、入力を複数のカテゴリに分類する必要があるニューラルネットワークの出力層にのみ使用されます。
softmaxのデメリット
・Softmaxは、クラス内のコンパクトなクラス間分離を必要としないため、大規模なマルチカテゴリタスクには適していません。
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/api_docs/python/tf/keras/activations/softmax
PyTorch
https://pytorch.org/docs/stable/generated/torch.nn.Softmax.html
GELU関数
GELU活性化関数は、Gaussian Error Linear Unit functionsの略称です。GELUはOpenAI GPTやBERTなどの有名なモデルで使われている活性化関数です。
GELUはReLU、ELU、PReLUなどのアクティベーションにより、シグモイドよりも高速で優れたニューラルネットワークの収束が可能になったと言われています。コツとしては、Dropoutに似た要素を入れている事です。Dropoutとは、いくつかのアクティベーションに0をランダムに乗算することにより、モデルを頑強します。
GELU定義
Geluは以下のように定義されます。
Computes gaussian error linear:
approximateがFalse場合は、
approximateがTrue場合は、
GELUの違い
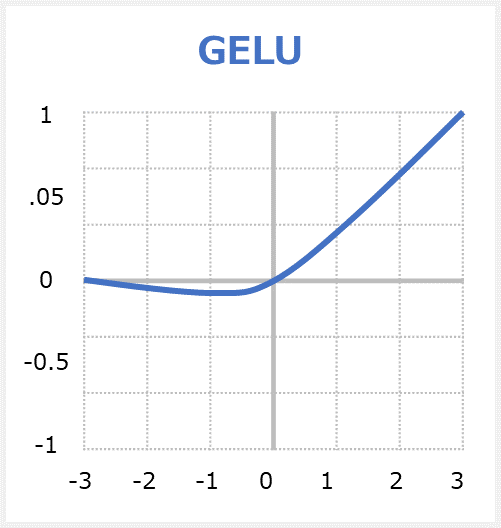
GELUとReLUとELUは非凸(non-convex)、非単調(non-monotonic)関数ですが、GELUは正の領域で線形ではなく、曲率があります。
GELUは単調増加ではありません。
GELUは確率的な要素を加味しています(Dropout)。
ライブラリ:
Tensorflow/Keras
https://www.tensorflow.org/addons/api_docs/python/tfa/activations/gelu#returns
PyTorch
https://pytorch.org/docs/stable/generated/torch.nn.GELU.html
論文:https://arxiv.org/abs/1606.08415
SELU関数
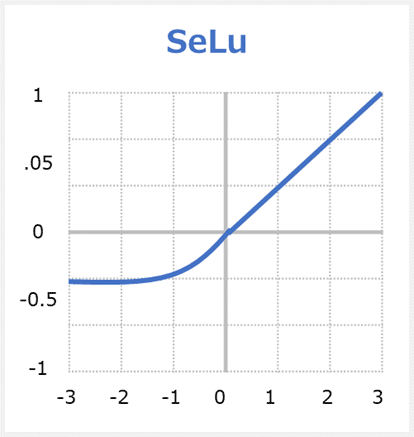
SELUはScaled Exponential Linear Unitsの英略称で、活性化関数の一つです。
SELUは勾配消失問題(Vanishing Gradient)を対応できます。何故ならばSELUは「0」を基点として、入力値が0以下なら「0」~「-λα」の間の値を、0より上なら「入力値をλ倍した値」を返します。ReLUおよびELUの拡張版です。
SELUの特徴
SELUはこの優れた自己正規化の品質を備えており、勾配消失を恐れる必要はありません。 今後、ReLUの代わりにSELUを使用する必要がある理由は3つあります。
1)ReLUと同様に、SELUは勾配消失に問題がないため、ディープニューラルネットワークを有効にします。
2)ReLUとは対照的に、Dying ReLUが起こりません(0以下での収束しない現象)。
3)SELUは、バッチ正規化と組み合わせた場合でも、他の活性化関数よりも速く、よりよく学習すると言われています。
ライブラリ:
論文:https://arxiv.org/pdf/1706.02515.pdf
Tensorflow: https://www.tensorflow.org/api_docs/python/tf/nn/selu
PyTorch: https://pytorch.org/docs/stable/generated/torch.nn.SELU.html
以上は代表的な活性化関数ですが、他にも以下があります。
FRelu関数
https://arxiv.org/abs/1706.08098
過去記事
KerasでのFReLU活性化関数
Selu関数
https://arxiv.org/abs/1706.02515v5
Relu6関数
https://arxiv.org/abs/1704.04861v1
Softsign関数
https://arxiv.org/pdf/1710.07654v3
Sifted Softsign関数
https://arxiv.org/pdf/1706.08566v5
KAF関数
https://arxiv.org/pdf/1707.04236v1
Tanexp関数
https://arxiv.org/pdf/2003.09855v2
ARiA関数
https://arxiv.org/abs/1805.08878v1
m-arcsinh関数
https://arxiv.org/pdf/2009.07530v1
Hermite 関数
https://arxiv.org/pdf/1909.05479v2
ELiSH関数
https://arxiv.org/pdf/1808.00783v1
Swish関数
https://arxiv.org/pdf/1710.05941
Mish関数
https://arxiv.org/abs/1908.08681
kWTA関数
https://arxiv.org/abs/1905.10510
HardTanh関数
https://nn.readthedocs.io/en/rtd/transfer/index.html#hardtanh
hardShrink関数
https://nn.readthedocs.io/en/rtd/transfer/index.html#hardshrink
softShrink関数
https://nn.readthedocs.io/en/rtd/transfer/index.html#softshrink
Noisy関数
https://arxiv.org/pdf/1603.00391.pdf
SoftMin関数
https://nn.readthedocs.io/en/rtd/transfer/index.html#softmin
SoftPlus関数
https://nn.readthedocs.io/en/rtd/transfer/index.html
LogSigmoid関数
https://nn.readthedocs.io/en/rtd/transfer/index.html#logsigmoid
LogSoftMax関数
https://nn.readthedocs.io/en/rtd/transfer/index.html#logsoftmax
https://pytorch.org/docs/stable/generated/torch.nn.LogSoftmax.html#torch.nn.LogSoftmax
CELU関数
https://pytorch.org/docs/stable/generated/torch.nn.CELU.html#torch.nn.CELU
SiLU関数
https://pytorch.org/docs/stable/generated/torch.nn.SiLU.html#torch.nn.SiLU
Threshold関数
https://pytorch.org/docs/stable/generated/torch.nn.Threshold.html#torch.nn.Threshold
Softmax2d関数
https://pytorch.org/docs/stable/generated/torch.nn.Softmax2d.html#torch.nn.Softmax2d
Softmax2d関数
https://pytorch.org/docs/stable/generated/torch.nn.Softmax2d.html#torch.nn.Softmax2d
AdaptiveLogSoftmaxWithLoss関数
Identity関数
https://pytorch.org/docs/stable/generated/torch.nn.Identity.html#torch.nn.Identity
関連記事
担当者:KW
バンコクのタイ出身 データサイエンティスト
製造、マーケティング、財務、AI研究などの様々な業界にPSI生産管理、在庫予測・最適化分析、顧客ロイヤルティ分析、センチメント分析、SaaS、PaaS、IaaS、AI at the Edge の環境構築などのスペシャリスト