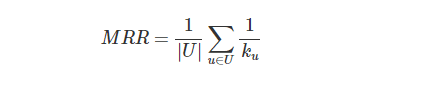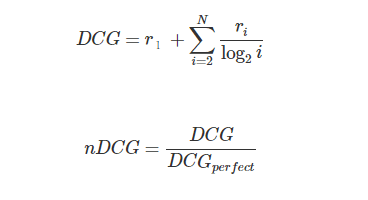レコメンドのランキングの評価指標 (PR曲線とAUC, MRR, MAP, nDCG)

1. ランキングの評価指標とは

ユーザに提示されるのはおすすめ度の高い上位数アイテム（TopN）複数であり、ユーザの嗜好が高いと思われる順にアイテムを正しく並べ変えるタスクと捉えることができます。

2. PR曲線（Precision-Recall Curve）

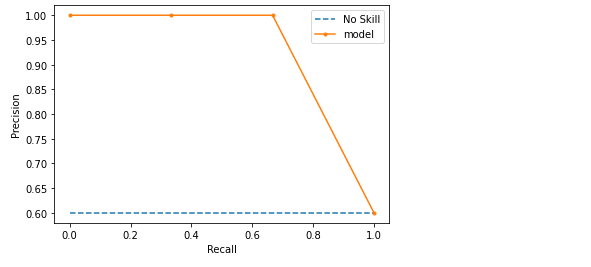
Recallを横軸に、Precisionを縦軸にとり、Top1、Top2,…というように閾値であるTopNの Nを変動させると、RecallとPrecisionが複数点プロットできます。精度が良いほど右上のほうに曲線は膨らんでいきます。さらに曲線と縦軸・横軸で囲まれる部分の面積がPR曲線の AUC(Area Under Curve) です。AUCはArea under the curveの略で、Area under an ROC curve（ROC曲線下の面積）をROC-AUCなどと呼びます。

各クラスのアイテム数がほぼ等しい場合は、ROC曲線を使用します。PR曲線は、不均衡データの評価の時に、よく使われます。

PR曲線のコード

サンプル予測結果を作成します。

import numpy as np

testy = np.array([1, 1, 0, 0, 1])

yhat = np.array([1, 1, 0, 0, 0])

probs = np.array([0.6, 0.5, 0.1, 0.1, 0.1])

PR曲線とAUCを作成します。

from sklearn.metrics import precision_recall_curve

from sklearn.metrics import f1_score

from sklearn.metrics import auc

from matplotlib import pyplot

# predict class values

lr_precision, lr_recall, _ = precision_recall_curve(testy, probs)

lr_f1, lr_auc = f1_score(testy, yhat), auc(lr_recall, lr_precision)

# summarize scores

print(‘predict: f1=%.3f auc=%.3f’ % (lr_f1, lr_auc))

# plot the precision-recall curves

no_skill = len(testy[testy==1]) / len(testy)

pyplot.plot([0, 1], [no_skill, no_skill], linestyle=’–‘, label=’No Skill’)

pyplot.plot(lr_recall, lr_precision, marker=’.’, label=’model’)

# axis labels

pyplot.xlabel(‘Recall’)

pyplot.ylabel(‘Precision’)

# show the legend

pyplot.legend()

# show the plot

pyplot.show()

predict: f1=0.800 auc=0.933

3. MRR（Mean Reciprocal Rank）

MMRはランキング評価の最も単純な計算方法です。レコメンドリストを上位から見て、最初の適合アイテムの順位をそのまま計算に利用したシンプルな指標で、以下の手順で算出されます。ユーザーで最後平均取っている点が特徴的な点です。

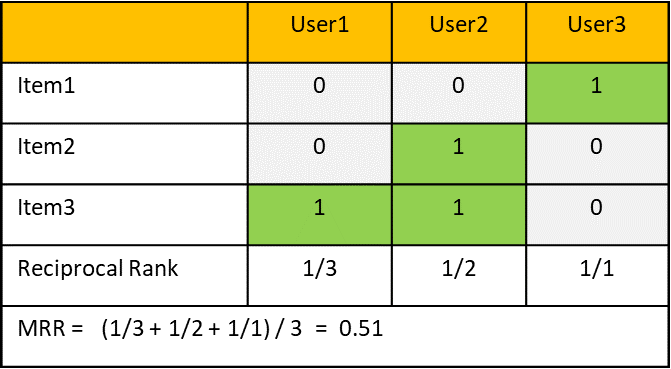
下記の例では、ユーザ1に最初の適合アイテムが出現する順位は3位です。Reciprocal Rankは1/3になります。その次はUser2, User3と全員分を計算し平均を取ります。

MRRの長所

・計算が簡単で、解釈も簡単です。

・リストの最初の関連要素に焦点を合わせます。「自分に最適なアイテム」を求めるユーザなど、ターゲットを絞った検索に最適です。

・ナビゲーションクエリや検索などの既知のアイテムの検索に適しています。

MRRの短所

・ MRRメトリックは部分的な所だけの計算になります。

・単一の関連アイテムを含むリストを、多くの関連アイテムを含むリストと同じくらいの重みで提供します。

・関連アイテムのリストを参照したいユーザーにとっては適切な評価指標ではない可能性があります。

MRRのコード

import numpy as np

def mean_reciprocal_rank(rs):

rs = (np.asarray(r).nonzero()[0] for r in rs)

return np.mean([1. / (r[0] + 1) if r.size else 0. for r in rs])

rs = [[0, 0, 1], [0, 1, 0], [1, 0, 0]]

mean_reciprocal_rank(rs)

0.611111111111111

4. MAP（Mean Average Precision）

MAPは特定のカットオフNまでの推奨アイテムのリスト全体を評価します。このカットオフは、以前はPrecision @Nメトリックを使用して組み込まれていました。MRRと比べるとPrecisionを考慮しています。

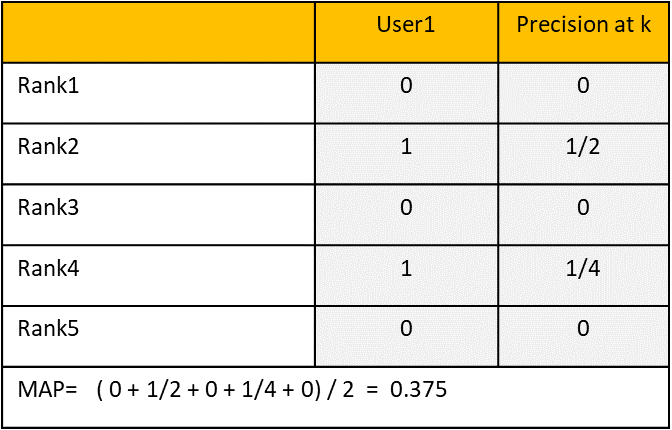
下記の例では、ユーザ1の適合アイテムはRank２とRank４になります。Top2、Top4でのPrecisionを求め、適合アイテムの数2で割って平均をとります。

MAPの長所

・適合率-再現率曲線の下の複雑な面積を表す単一のメトリックを提供します。これにより、リストごとの平均精度が提供されます。

・リストのおすすめアイテムのランキングを自然に処理します。

・推奨リストの上位で発生するエラーにより大きな重みを与えることができます。

MAPの短所

・バイナリ評価に適しています。ただし、きめ細かい数値評価には適していません。このメトリックは、この情報からエラーがありません。

・評価では、バイナリの関連性を作成するために、最初に評価をしきい値設定する必要があります。これにより、手動のしきい値が原因で、評価メトリックにバイアスが生じます。

MAPのコード

import numpy as np

def precision_at_k(r, k):

assert k >= 1

r = np.asarray(r)[:k] != 0

if r.size != k:

raise ValueError(‘Relevance score length < k’)

return np.mean(r)

def average_precision(r):

r = np.asarray(r) != 0

out = [precision_at_k(r, k + 1) for k in range(r.size) if r[k]]

if not out:

return 0.

return np.mean(out)

def mean_average_precision(rs):

return np.mean([average_precision(r) for r in rs])

rs = [[1, 1, 0, 1, 0, 1, 0, 0, 0, 1]]

mean_average_precision(rs)

0.7833333333333333

5. nDCG（normalized Discounted Cumulative Gain）

MAPメトリックは、NDCGメトリックの目標に似ています。関連性の高いドキュメントは、推奨リストの上位にあります。ただし、NDCGは、推奨リストの評価をさらに調整します。nDCGはDCGという指標を正規化したものなのですが、DCGは一言でいうとアイテムをおすすめ順に並べた際の実際のスコアの合計値です。

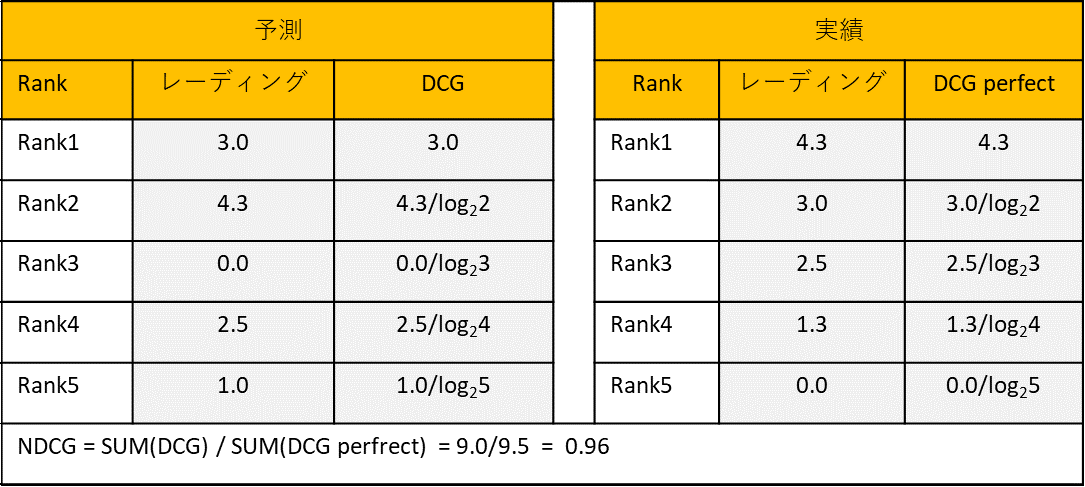
下記の例では、ユーザの予測したレーディングと実際のレーディングで下記のようにNDCGを計算します。

NDCGの長所

・レーディングの関連性の値が考慮されます。

・ランク付けされたアイテムの位置を評価します。

・滑らかな対数割引係数は、経験則的に上手くいく事が多い。

NDCGの短所

・部分的なフィードバックに関するいくつかの問題。これは、評価が不完全な場合に発生します。

・IDCGがゼロに等しい場合、ユーザーは手動で処理する必要があります。これは、ユーザーが関連するドキュメントを持っていない場合に発生します。

・recsysシステムによって返されるランク付けされたリストのサイズはK未満にすることができます。これを処理するために、固定サイズの結果セットを検討し、小さいセットに最小スコアを埋め込むことができます。

nDCGのコード

import numpy as np

def dcg_at_k(r, k):

r = np.asfarray(r)[:k]

if r.size:

return np.sum(np.subtract(np.power(2, r), 1) / np.log2(np.arange(2, r.size + 2)))

return 0.

def ndcg_at_k(r, k):

idcg = dcg_at_k(sorted(r, reverse=True), k)

if not idcg:

return 0.

return dcg_at_k(r, k) / idcg

r = [3, 2, 3, 0, 0, 1, 2, 4, 3, 1]

ndcg_at_k(r, 1)

0.4666666666666667

担当者：KW
バンコクのタイ出身　データサイエンティスト
製造、マーケティング、財務、AI研究などの様々な業界にPSI生産管理、在庫予測・最適化分析、顧客ロイヤルティ分析、センチメント分析、SaaS、PaaS、IaaS、AI at the Edge の環境構築などのスペシャリスト

目次

1. ランキングの評価指標とは

2. PR曲線（Precision-Recall Curve）

3. MRR（Mean Reciprocal Rank）

4. MAP（Mean Average Precision）

5. nDCG（normalized Discounted Cumulative Gain）