前回の記事は線形回帰を解説しました。
回帰分析の説明はこの記事を参考してください。
線形回帰
回帰分析を行うとき、 Scikit-learn と Statsmodelsのライブラリをよく使います。前回はScikit-learnで回帰分析を行いました。今回はScikit-learnとStatsmodelsのライブラリを比較して、回帰分析を解説・実験します。
目次:
1. ライブラリ
1.1 Scikit-learnの回帰分析
1.2 Statsmodelsの回帰分析
2. コード・実験
2.1 データ準備
2.2 Sklearnの回帰分析
2.3 Statsmodelsの回帰分析
2.4 結果の説明
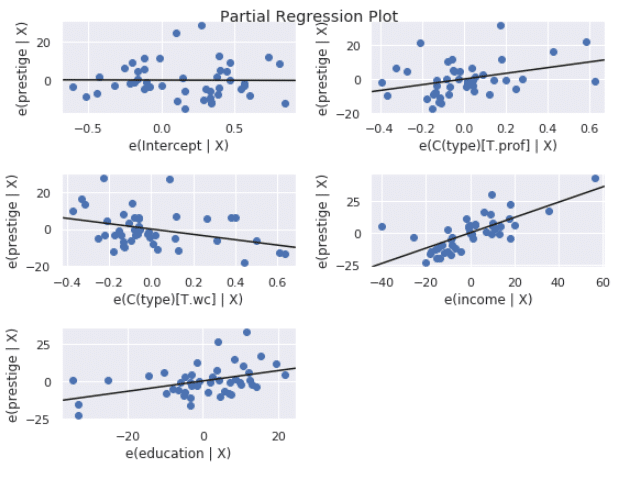
3. Partial Regression Plots
4.まとめ
1.ライブラリ
1.1 Scikit-learnの回帰分析
sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
パラメータ設定:
fit_intercept : boolean, optional, default True:
False に設定すると切片を求める計算を含めません。
normalize : boolean, optional, default False:
True に設定すると、説明変数を事前に正規化します。
copy_X : boolean, optional, default True:
メモリ内でデータを複製してから実行するかどうか。
n_jobs : int or None, optional (default=None)
計算に使うジョブの数。-1 に設定すると、すべての CPU を使って計算します。
1.2 Statsmodelsの回帰分析
statsmodels.regression.linear_model.OLS(formula, data, subset=None)
アルゴリズムのよって、パラメータを設定します。
・OLS Ordinary Least Squares 普通の最小二乗法
・WLS Weighted Least Squares 加重最小二乗法
・GLS Generalized Least Squares 一般化最小二乗法
モデル式の文法
R-styleの共用を考えています。
モデル式の例:
y ~ x 回帰モデル,yはxにより説明される
y ~ x1 + x2 重回帰モデル,yは,独立変数 x1 と x2 により説明される
y ~ 1 + x1 + x2 y は,(切片 / intercept と)x1,x2 で説明される
質的変数の場合はN-1の変数になります。
data はpandasのデータフレームです。
2.コード・実験
概要:
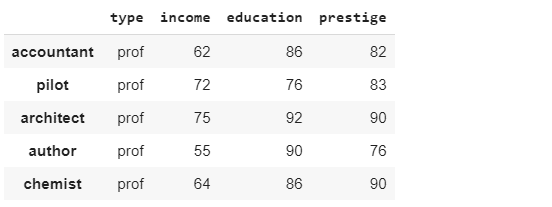
データセット:Duncan’s Occupational Prestige Data:Duncanは、45行と4列があり、1950年の米国の職業の威信およびその他の特性に関するデータセットです。
環境:google colab Python3 GPU
ライブラリ: Statsmodels
pip install -U statsmodels
モデル:
実験:重回帰分析
モデル評価:R2
2.1 データ準備
ライブラリ
import matplotlib.pyplot as plt import seaborn as sns; sns.set() import numpy as np import statsmodels.api as sm from statsmodels.formula.api import ols
データセットロード
df = sm.datasets.get_rdataset("Duncan", "carData", cache=True).data
df.head()グラフ作成
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
x1 = df.type
x2 = df.income
x3 = df.education
y = df.prestige
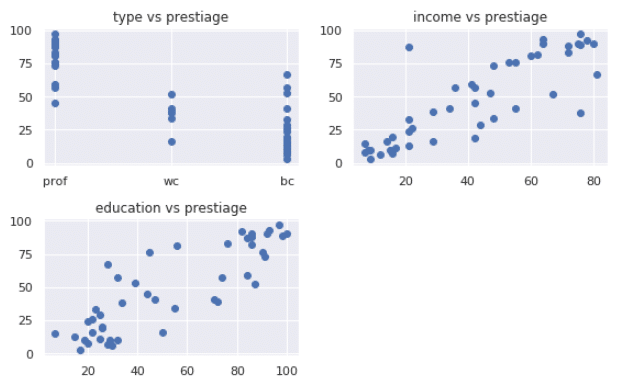
fig = plt.figure(figsize=(8,5))
plt.subplot(2,2,1)
plt.plot(x1, y, 'o')
plt.title("type vs prestiage")
plt.subplot(2,2,2)
plt.plot(x2, y, 'o')
plt.title("income vs prestiage")
plt.subplot(2,2,3)
plt.plot(x3, y, 'o')
plt.title("education vs prestiage")
plt.tight_layout()2.2 Sklearnの回帰分析
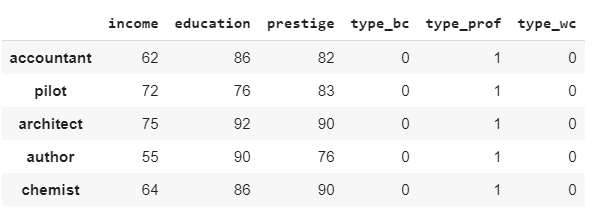
ダミー変数に変更
ダミー変数の詳細は下記の記事をご覧ください。
ダミー変数に変換 【One-Hotエンコーディング】
import pandas as pd df2 = pd.get_dummies(df) df2.head()
Sklearnの回帰分析の学習
from sklearn.linear_model import LinearRegression
x = df2.loc[:, df2.columns != 'prestige']
y = df2[['prestige']]
reg_mod = LinearRegression(fit_intercept=True)
reg_mod.fit(x, y)
print(" r2: ", reg_mod.score(x, y))
print(" Coef: ", reg_mod.coef_[0])
print(" intercept: ", reg_mod.intercept_[0])r2: 0.9130657009984509
Coef: [ 0.5975465 0.34531933 -0.66546001 15.99205339 -15.32659337]
intercept: 0.48043218310085223
2.3 Statsmodelsの回帰分析
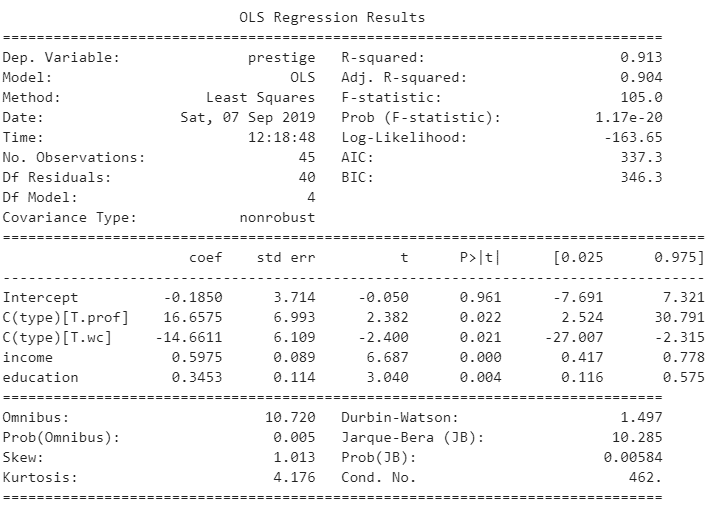
olsmod = ols(formula="prestige ~ C(type) + income + education", data=df).fit() print(olsmod.summary())
2.4 結果の説明
結果を確認すると、モデルの係数a(T.prof)とモデルの係数b(T.wc)とモデルの係数c(income)と 係数d(education)と定数e(const)はそれぞれ、+16.65, -14.66, +0.59, +0.34, -0.18となることが分かります。よって、このモデルは以下の数式で表すことができます。
[prestige]=[T.prof]×16.6575 -[T.wc]×14.6611 +[income]×0.5975 +[education]×0.3453 –0.1850
決定係数(R-squared: 0.913)は90%以上であり、よく当てはまっているといえます。
F検定(F-stat: 105, p-value: 1.17e-20)が十分に大きく、有意確率(p-value)も十分に小さいので、モデル全体として妥当であると判断できます。
t検定(係数1 T.prof:t-stat= 2.382、p-value=0.022
係数1 T.wc:t-stat= -2.400、p-value=0.021
係数1 income:t-stat= 6.687、p-value=0.000、
係数2 education:t-stat= 3.040、p-value=0.004、
定数 const:t-stat= -0.050、p-value=0.961)
係数T.prof、係数T.wc、係数income、係数education、定数constの有意確率双方とも十分に小さい値であり係数、定数とも妥当であると判断できます。
summaryのレポートを出力しなくて、特定の値を出力することができます。
print('Parameters: ', olsmod.params)
print('R2: ', olsmod.rsquared)3. Partial Regression Plots
fig = plt.figure(figsize=(8,6)) fig = sm.graphics.plot_partregress_grid(olsmod, fig=fig) plt.tight_layout()
4. まとめ
今回はPythonのSci-kit learnとStatsmodelsのライブラリで重回帰分析を行いました。Statsmodelsのライブラリは自動でダミー変数を変換し、詳細の結果ができるし、グラフも簡単に作成してもるし、統計量が多いため統計解析に有利なライブラリです。