前回の記事は「Mnistで深層学習入門 活性化関数 時間/精度比較」でrelu, tanh, sigmoid, eluのパラメーターでの結果を比較しました。今回の記事は正則化について解説します。
KerasからMnistのデータセットの深層学習モデルを実験します。
import numpy as np
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.optimizers import SGD
from sklearn import datasets
from sklearn.model_selection import train_test_split
from tensorflow.examples.tutorials.mnist import input_data
%matplotlib inline
import matplotlib.pyplot as plt
mnist = input_data.read_data_sets(‘MNIST_data’, one_hot=True)
Extracting MNIST_datatrain-images-idx3-ubyte.gz
Extracting MNIST_datatrain-labels-idx1-ubyte.gz
Extracting MNIST_datat10k-images-idx3-ubyte.gz
Extracting MNIST_datat10k-labels-idx1-ubyte.gz
8,000件の学習データと2,000件のテストデータに分けます。数のデータは748
(28×28)になります。
Yは0から9までのデータセットです。
n = len(mnist.train.images)
N = 10000 # MNISTの一部を使う
indices = np.random.permutation(range(n))[:N] # ランダムにN枚を選択
X = mnist.train.images[indices]
y = mnist.train.labels[indices]
X_train, X_test, Y_train, Y_test = train_test_split(X, y, train_size=0.8)
X_train.shape, X_test.shape, Y_train.shape, Y_test.shape
((8000, 784), (2000, 784), (8000, 10), (2000, 10))
次にニューラルネットワークの構成を作成します。
784ノードの入力ノードから30個のDenseノートに繋がります。
784 * 30 = 23520パラメータになります。
from keras.models import Sequential
from keras.layers.core import Activation, Dense
from keras import backend as K
from keras import regularizers
n_in = len(X[0])
n_hidden = 30
n_out = len(y[0])
alpha = 0.01
model = Sequential()
model.add(Dense(n_hidden, input_dim = n_in,
# kernel_regularizer = regularizers.l2(0.2),
# activity_regularizer=regularizers.l1(0.05)
))
model.add(Dense(n_out))
model.add(Activation(‘softmax’))
model.compile(loss=’categorical_crossentropy’,
optimizer=SGD(lr=0.01),
metrics=[‘accuracy’])
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param # =================================================================]
dense_219 (Dense) (None, 30) 23550 _________________________________________________________________
dense_220 (Dense) (None, 10) 310 _________________________________________________________________
activation_131 (Activation) (None, 10) 0 =================================================================
Total params: 23,860
Trainable params: 23,860
Non-trainable params: 0
_________________________________________________________________
import time
start = time.time()
epochs = 50
batch_size = 200
history = model.fit(X_train, Y_train,
epochs=epochs,
batch_size=batch_size,
validation_split=0.2,
verbose=0)
loss_and_metrics = model.evaluate(X_test, Y_test)
print(loss_and_metrics)
end = time.time()
2000/2000 [==============================] - 0s 30us/step[0.4303508236408234, 0.8825]
# summarize history for accuracy
plt.plot(history.history[‘acc’])
plt.title(‘model accuracy’)
plt.ylabel(‘accuracy’)
plt.plot(history.history[‘val_acc’])
plt.xlabel(‘epoch’)
plt.legend([‘train’, ‘test’], loc=’upper left’)
plt.text(.94, .01, (‘time:%.2fs’ % (end – start)).lstrip(‘0’),
transform=plt.gca().transAxes, size=12,
horizontalalignment=’right’)
plt.text(.10, .01, (‘max test acc: %.2f’% max(history.history[‘val_acc’])),
transform=plt.gca().transAxes,
size=12, horizontalalignment=’left’)
plt.show()
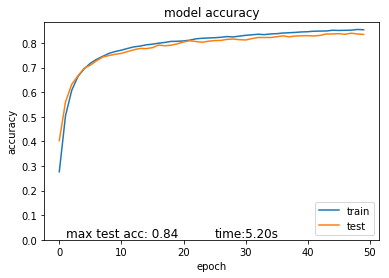
緻密層30正則化なしの結果はテストデータの精度0.88です。
正則化の利用
正則化によって,最適化中にレイヤーパラメータあるいはレイヤーの出力に制約を課すことができます.これらの正則化はネットワークが最適化する損失関数に組み込まれます。
L1ノルム正則化項
- L1正則化は重み付け要素w1=0で、「不要なパラメータを削ると次元・特徴量削減」と言われて正則化です。
- 変数間に強い相関があると、相関を捉えられず適切に変数を選択できない可能性があります。
L2ノルム正則化項
- w1, w2は原点を中心とした円の領域を取ります。L2正則化は「過学習を抑えて汎用化したい」という時によく使われます。
- L2正則化項は微分が可能なため、解析的に解ける。L1正則化項は解析的に解けません。
正則化の詳細はこちれです。
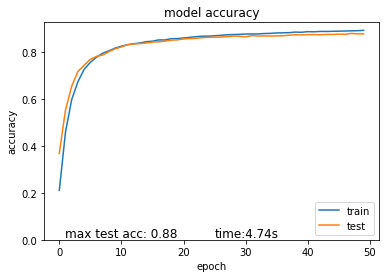
緻密層30と0.05のL2正則化の結果はテストデータの精度0.86にしまいります。
model.add(Dense(n_hidden, input_dim = n_in, activation=’relu’
kernel_regularizer = regularizers.l2(0.05)))
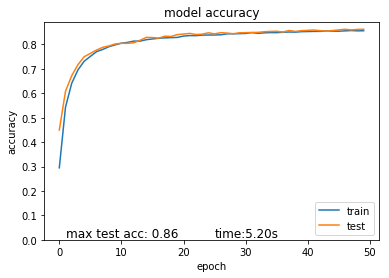
L2正則化の結果は0.02になると、制度は89になります。
model.add(Dense(n_hidden, input_dim = n_in, activation=’relu’
kernel_regularizer = regularizers.l2(0.02)))
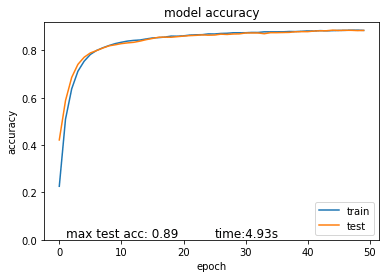
0.0001のL1正則化の変更なると、制度は89に上がりました。
model.add(Dense(n_hidden, input_dim = n_in,
activity_regularizer=regularizers.l1(0.0001)))
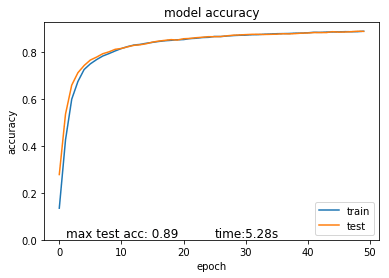
0.0001のL1正則化の変更なると、制度は89に上がりました。
model.add(Dense(n_hidden, input_dim = n_in,
activity_regularizer=regularizers.l1(0.0001)))