前回の記事は「時系列データの特徴」を説明しました。今回の記事は時系列データの評価方法を説明します。
モデル機械を評価するために、データを学習データとテストデータに分割することがよく使われています。学習データはモデルを作成し、テストデータはモデルの評価に使用されます。順番がシャッフルされてしまうため、時系列データに対しては使いにくいという問題がありました。各観測は従属的であるため、それらをランダムにグループに分割することはできません。 また、データリーケージ(Data leakage)の問題も発生します。
データリーケージ(Data leakage)
データリーケージとは、モデルを作成るときに、本来知らないはずの情報(変数やデータ)を不当に使ってしまうことです。 手元のデータでは高い精度が出たのに、本番環境ではまったく精度が出ない、といった事態になります。
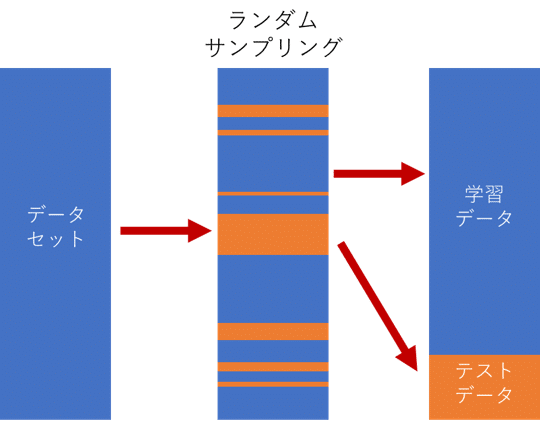
3つの時系列データモデルの評価方法を説明します。
1)Train-Test Splits:時間的順序を考慮した学習・テスト分割
2)Multiple Train-Test Splits:時間的順序を考慮した複数の学習・テスト分割
3)Walk-Forward Validation
ではモデル評価の比額を実験しましょう。
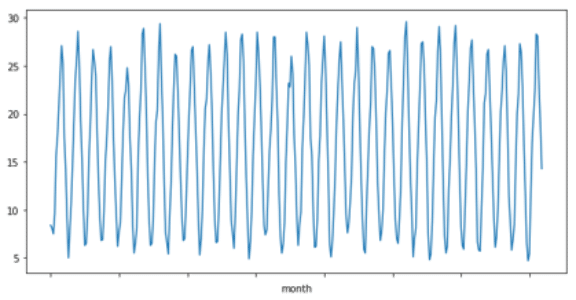
東京の日平均気温の月平均値(℃)
1988年12月から2018年11月まで30年の月次気温データ(360件)
# sunspotデータロード
from pandas import Series
from matplotlib import pyplot
series = Series.from_csv(‘ tokyou_temp.csv’, header=0)
print(series.head())
series.plot()
pyplot.show()
month
Dec-88 8.4
Jan-89 8.1
Feb-89 7.5
Mar-89 9.6
Apr-89 15.6
Name: temp, dtype: float64
1)時間的順序を考慮した学習・テスト分割
2つの時間枠に分割して、学習データとテストデータを分けることができます。
# 80% 学習 20%テスト
X = series.values
train_size = int(len(X) * 0.8)
train, test = X[0:train_size], X[train_size:len(X)]
print(‘Observations: %d’ % (len(X)))
print(‘Training Observations: %d’ % (len(train)))
print(‘Testing Observations: %d’ % (len(test)))
pyplot.plot(train)
pyplot.plot([None for i in train] + [x for x in test])
pyplot.show()
Observations: 360
Training Observations: 288
Testing Observations: 72
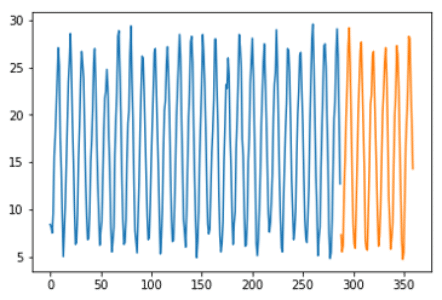
青い色は学習データ、緑色はテストデータです。
2)Multiple Train-Test Splits:時間的順序を考慮した複数の学習・テスト分割
複数のモデルの学習とテストが必要になりますが、この追加の計算コストは、見えないデータに対する選択された方法と構成の予想されるパフォーマンスのより堅牢な見積もりを提供します。
scikit-learnのライブラリーのTimeSeriesSplitで、グループの数を設定することができます。
training_size = i * n_samples / (n_splits + 1) + n_samples % (n_splits + 1)
test_size = n_samples / (n_splits + 1)
データセットに対して3つの分割を作成しましょう。 上記と同じ計算を使用すると、次の電車とテストの分割が作成されることが期待されます。
Split 1: 90 train, 90 test
Split 2: 180 train, 90 test
Split 3: 270 train, 90 test
from sklearn.model_selection import TimeSeriesSplit
splits = TimeSeriesSplit(n_splits=3)
pyplot.figure(1)
index = 1
for train_index, test_index in splits.split(X):
train = X[train_index]
test = X[test_index]
print(‘Observations: %d’ % (len(train) + len(test)))
print(‘Training Observations: %d’ % (len(train)))
print(‘Testing Observations: %d’ % (len(test)))
pyplot.subplot(310 + index)
pyplot.plot(train)
pyplot.plot([None for i in train] + [x for x in test])
index += 1
pyplot.show()
Observations: 180
Training Observations: 90
Testing Observations: 90
Observations: 270
Training Observations: 180
Testing Observations: 90
Observations: 360
Training Observations: 270
Testing Observations: 90
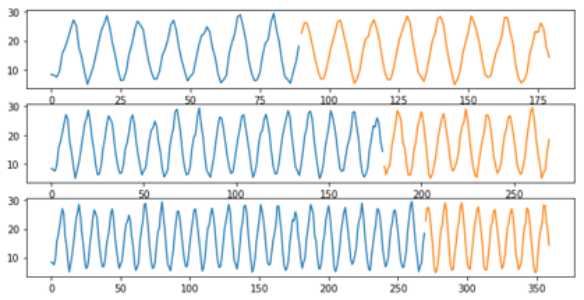
こ方法の限界は、学習されたモデルがテストセットの各評価で評価されるときに固定されたままであることです。
毎日または毎月の新しい観察が利用可能になると、モデルを再トレーニングすることができるので、現実的ではない可能性がある。 この問題は、次の方法は解決することができます。
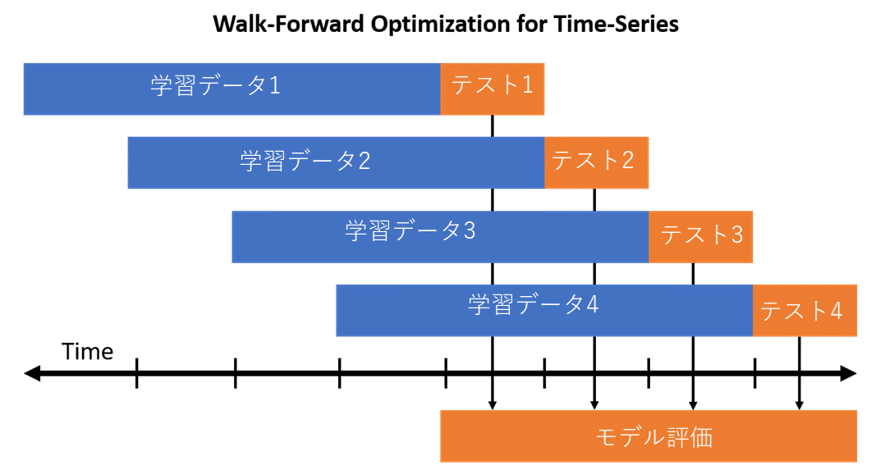
Walk Forward Validation
モデルは各時間ステップで良好な予測を行う最良の機会になります。 この前提のもとで、私たちは機械学習モデルを評価することができます。
2つの設定
1.観察の最小回数。 まず、モデルを訓練するのに必要な観測の最小数を選択する必要があります。 これは、スライディングウインドウが使用される場合のウインドウ幅と考えることができる(次の点を参照)。
2.スライディングまたは拡大ウィンドウ。 次に、利用可能なすべてのデータに対してモデルを訓練するか、直近の観測でのみ訓練するかを決定する必要があります。 これは、スライドまたは拡大ウィンドウを使用するかどうかを決定します。
この方法では、時系列の一度に1歩ずつ移動する必要があるため、Walk Forward TestingまたはWalk Forward Validationと呼ばれます。
from pandas import Series
from matplotlib import pyplot
series = Series.from_csv(‘tokyou_temp.csv’, header=0)
X = series.values
n_train = 180
n_records = len(X)
for i in range(n_train, n_records):
train, test = X[0:i], X[i:i+1]
print(‘train=%d, test=%d’ % (len(train), len(test)))
train=180, test=1
train=181, test=1
train=182, test=1
…
train=359, test=1
実際に選択されたモデリング方法およびパラメータがどのように実行されるかをはるかに良好に評価できるという利点があります。 この改善された見積もりは、非常に多くのモデルを作成するための計算コストにかかっています。

Pingback: DTW(Dynamic Time Warping)動的時間伸縮法 - S-Analysis