ロジスティック回帰

全て, 統計解析


前回の記事は線形回帰を説明しました。この記事では、回帰分析群のロジスティック回帰お話になります。

ロジスティック回帰とは

ロジスティック回帰とは、2群で分けられた目的変数に対する，1つ以上の説明変数の影響を調べ、機械学習分類アルゴリズムです。ロジスティック回帰は、2群分類の最も簡単で一般的に使用される機械学習アルゴリズムの1つです。 実装が容易で、バイナリ分類の問題のベースラインとして使用できます。 ロジスティック回帰は、さまざまな分類問題に使用できます。 例えば、糖尿病の予測、チャーン分析、キャンペーンの応答など。 では、ロジスティック回帰のモデルを作成しましょう。 まず、データセットを作成します。

 

#ライブラリー

import matplotlib.pyplot as plt

import pandas as pd

from scipy import stats

import seaborn as sns

#サンプルデータ作成

distA = stats.norm(30, 5)

distB = stats.norm(15, 4)

data = []

for i in range(100):

    data.append((distA.rvs(), “A”))

    data.append((distB.rvs(), “B”))

df = pd.DataFrame(data, columns=[“measurement”, “class”])

#データを表示する

print(df.head())

#ヒストグラムの図作成

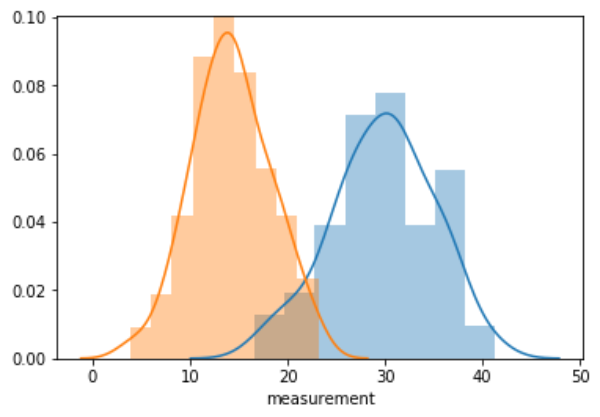
sns.distplot(df[df[“class”] == “A”][“measurement”])

sns.distplot(df[df[“class”] == “B”][“measurement”])

sns.plt.show()

logistic_regression_2

   measurement class

0    28.271342     A

1    14.206356     B

2    18.979297     A

3    14.925955     B

4    27.999255     A

 

AクラスとBクラスのデータセットを作成しました。

では、sklearnのライブラリーでモデルを作成します。

from sklearn import linear_model

 

#データ加工

df[“class_num”] = df[‘class’].apply(lambda x: 1 if x == ‘A’ else 0 )

df.sort_values(by=”measurement”, inplace=True)

 

#モデルの学習

X = df[[“measurement”]]

y = df[“class_num”]

model = linear_model.LogisticRegression()

model.fit(X, y)

 

#図を作成します。

plt.scatter(df[“measurement”], df[“class_num”])

plt.plot(df[“measurement”], model.predict_proba(X)[:, 1], color=”r”)

plt.xlabel(“Measurement”)

plt.ylabel(“Probability of being in class B”)

plt.show()

 

#制度の計算

print “Accuracy”, model.score(X, y)

logistic_regression_3

 

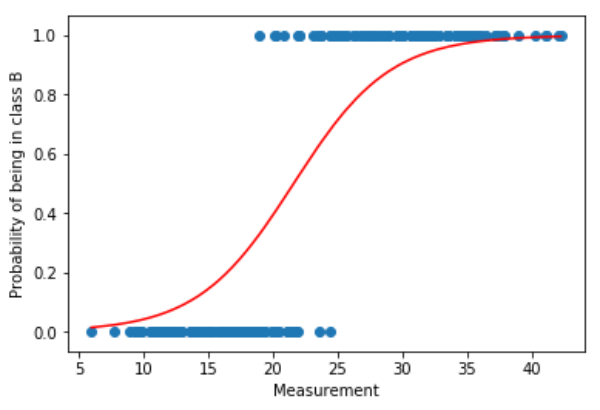
Accuracy 0.955

 

このロジスティック回帰モデルは95％の精度で2クラスを良く分離することができます。

 

詳細：

http://scikit-learn.org/stable/modules/linear_model.html#logistic-regression