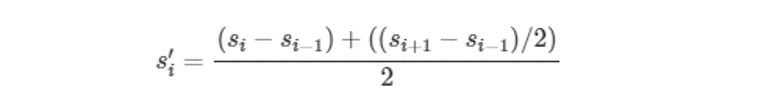前回「時系列データの評価方法」について解説しました。
時系列データの向け、時系列同士の類似度を測る際にDTWという手法があります。今回の記事はDTW(Dynamic Time Warping)/動的時間伸縮法について解説したいと思います。
目次
1. DTWの概要
___1.1 DTW(Dynamic Time Warping)/動的時間伸縮法とは
___1.2 DTWの計算
2. tslearn.clusteringの説明
___2.1 tslearn.clusteringのクラス
___2.2 パラメタの説明
3. 実験
___3.1 データ理解
___3.2 EuclideanとDTWのk-meansクラスター
___3.3 可視化
4. まとめ
1. DTWの概要
1.1 DTW(Dynamic Time Warping)/動的時間伸縮法とは
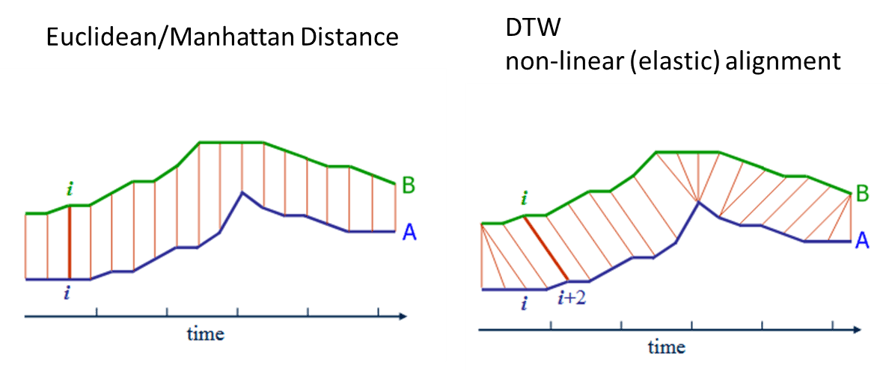
DTWとは時系列データ同士の距離・類似度を測る際に用いる手法です。波形の距離を求める手法としてはユークリッド距離(Euclidean Distance)や マンハッタン距離等(Manhattan distance)があるかと思います。
DTWは2つの時系列の各点の距離(誤差の絶対値)を総当たりで求め、全て求めた上で2つの時系列が最短となるパスを見つけます。時系列同士の長さや周期が違っても類似度を求めることができます。
1.2 DTWの計算
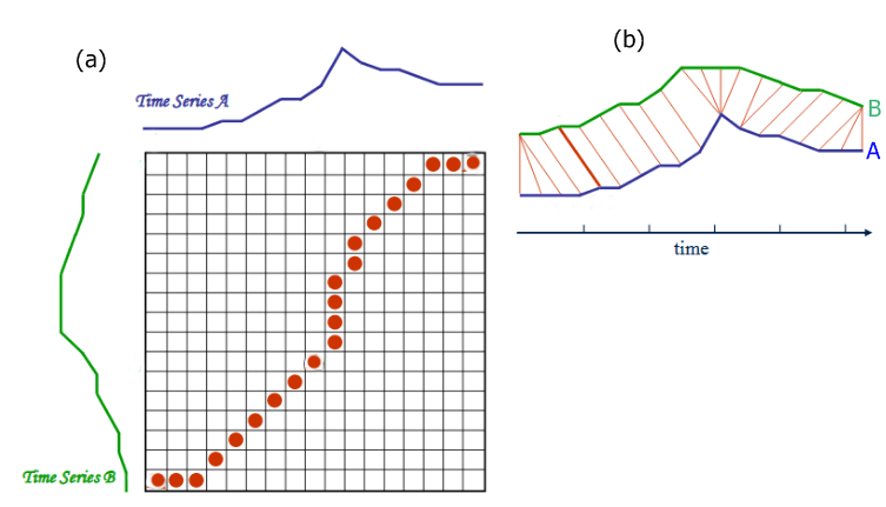
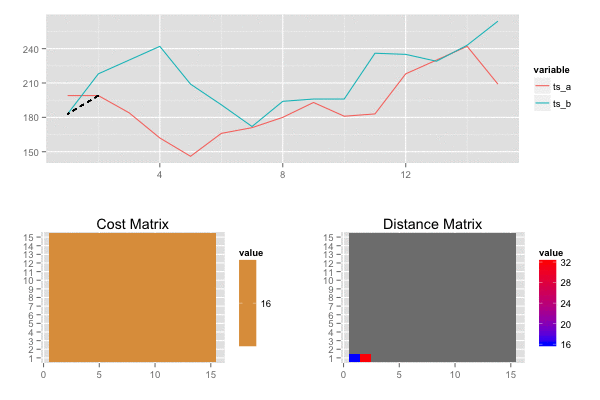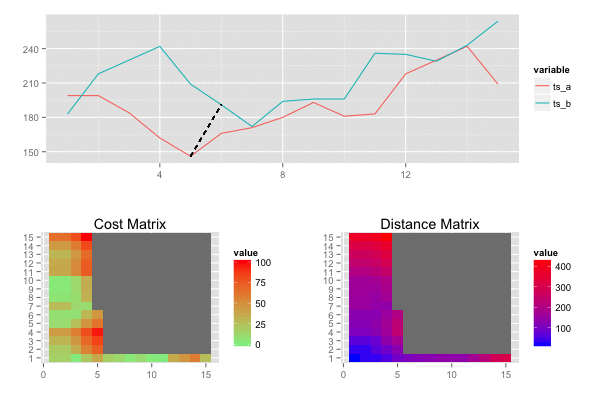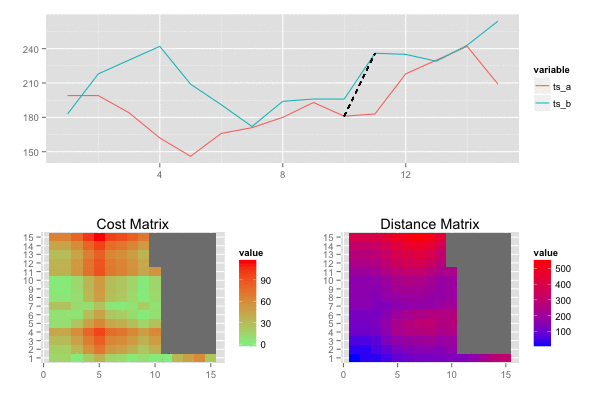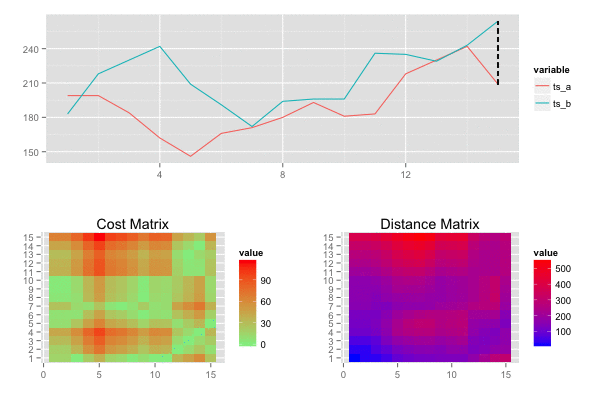
類似度を算出したい2つの時系列データ S=s1,s2,…,sm,T=t1,t2,…,tn, があるとき,各時系列データを横・縦に並べたグリッドを考えることができる. このグリッドの点 (i,j)は要素siとtj間のアライメントに相当します。
ワーピングパス W=w1,w2,⋯,wk は 時系列データSとTの各要素を”距離”が小さくなるようにアライメントします。つまり,Wはグリッドの点の系列となります。
Derivative DTW
Derivative DTWは時系列データ
S=s1,s2,⋯,smの各要素に対して,次のような変換を行った時系列データS′=s′1,s′2,…,s′mをりようします。
DTWでは各点同士の比較にとどまっていたのに対して,この変換により,上昇トレンドや下降トレンドなどの形状を考慮した類似度が算出できるため,DTWより形状を考慮した時系列データ間の距離が算出でできます。
2. tslearn.clusteringの説明
2.1 tslearn.clusteringのクラス
tslearn.clustering.TimeSeriesKMeans
class tslearn.clustering.TimeSeriesKMeans(n_clusters=3, max_iter=50, tol=1e-06, n_init=1, metric=’euclidean’, max_iter_barycenter=100, metric_params=None, n_jobs=None, dtw_inertia=False, verbose=0, random_state=None, init=’k-means++’)
2.2 パラメタの説明
n_clusters : int (default: 3)
クラスターの個数
max_iter : int (default: 50)
アルゴリズムの内部の最大イテレーション回数
tol : float (default: 1e-6)
収束と判定するための相対的な許容誤差
n_init : int (default: 1)
異なるセントロイドの初期値を用いたk-meansあるゴリmズムの実行回数
metric : {“euclidean”, “dtw”, “softdtw”} (default: “euclidean”)
Euclidean、dtw、softdtwの距離のアルゴリズムを選択することができます。
max_iter_barycenter : int (default: 100)
”dtw” の ”softdtw”のmetricのため、バリセンターのイテレーション回数
metric_params : dict or None (default: None)
交差距離の並列化の設定
n_jobs : int or None, optional (default=None)
クロスディスタンスマトリックス計算のために並行して実行するジョブの数。
Noneは、joblib.parallel_backendコンテキストの場合を除き、1のプロセッサを使用します。 -1は、すべてのプロセッサを使用します。
dtw_inertia: bool (default: False)
DTWが選択されたメトリックではない場合でも、DTW慣性を計算するかどうか。
verbose : int (default: 0)
ゼロ以外の場合、モデルの学習中に慣性に関する情報を出力し、joblibの進行メッセージが出力されます。
random_state : integer or numpy.RandomState, optional
セントロイドの初期化に用いる乱数発生器の状態
init : {‘k-means++’, ‘random’ or an ndarray} (default: ‘k-means++’)
‘k-means++’と ‘random’ のクラスターのアルゴリズムを選択することができます。
3. 実験
環境:google colab
データセット:12アイテムの24ヶ月の時系列データ
モデル:EuclideanとDTWのk-means++クラスター
データが含まれる空間にk個の点(セントロイド)に最も近いかを計算して、そのデータが所属するクラスタとします。k-means++法は標準的なk-means法の反復を行う前にクラスタ中心を初期化するプロセスを行うので、空間計算量を悪化せず k-means を高速化する手法です。
k-means++の詳細はこちらです。
3.1 データ理解
tslernのライブラリをインストールします。
!pip install tslearn
今回はgoogle colabを接続します。
from google.colab import drive
drive.mount('/content/drive')今回はgoogle colabを接続します。
from google.colab import drive
drive.mount('/content/drive')先ず入力データを確認します。
%ls "/content/drive/My Drive/dataset/time/"
data.csv
データを読み込んでデータフレームを作成します。
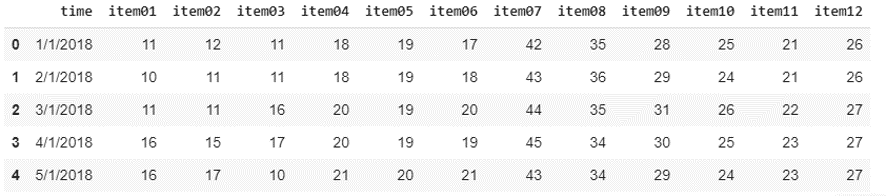
import numpy as np import pandas as pd seed = 111 input_path = "/content/drive/My Drive/dataset/time/data.csv" df = pd.read_csv(input_path, header=0) df.head(5)
データフレームの行列数を確認します。
12アイテム、24ヶ月の時系列データデータです。
df.shape
(24, 13)
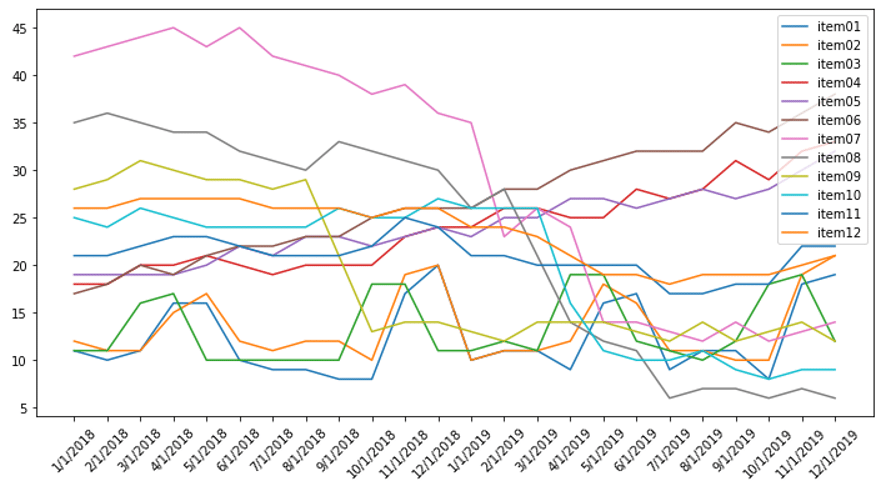
データ可視化を行います。
折れ線グラフで12このアイテムを表示します。
import matplotlib.pyplot as plt from pylab import rcParams item_list = df.columns.tolist()[1:] rcParams["figure.figsize"]= 12,6 fig = plt.figure(1) ax = fig.add_subplot(111) for item in item_list: plt.plot(df["time"], df[item], label=item) ax.set_xticklabels(df["time"], rotation = 45) plt.legend() plt.show()
3.2 EuclideanとDTWのk-meansクラスター
学習データ作成
X_train = df.loc[:, df.columns != 'time']
Euclidean k-meansを行います。
# Euclidean k-means
from pylab import rcParams
from tslearn.clustering import TimeSeriesKMeans
from datetime import datetime
start_time = datetime.now()
print("Euclidean k-means")
km = TimeSeriesKMeans(n_clusters=3, verbose=True, random_state=seed)
y_pred = km.fit_predict(X_train.T)
print(y_pred)
end_time = datetime.now()
print('Duration: {}'.format(end_time - start_time))Euclidean k-means
700.333 –> 471.261 –> 471.261 –>
[2 2 2 0 0 0 1 1 1 1 0 1]
Duration: 0:00:00.009303
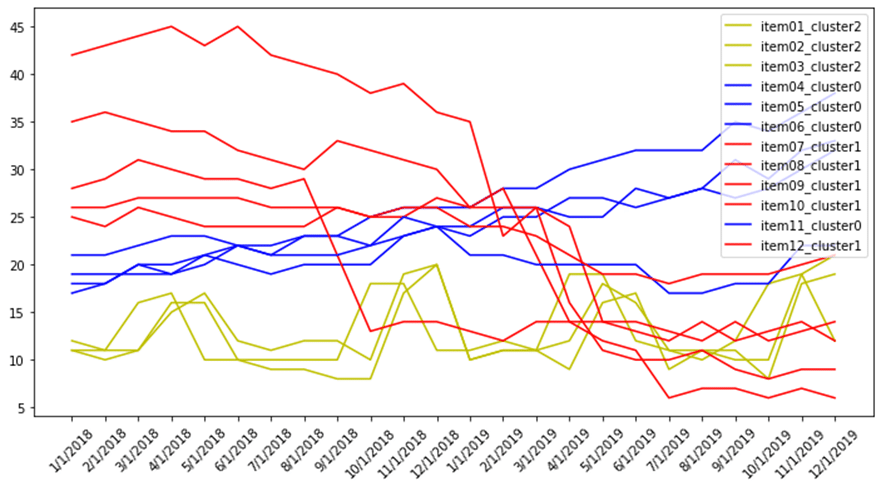
3.3 可視化
色で3つのクラスターに分けました。
クラスタがちゃんとできました。
import matplotlib.pyplot as plt from pylab import rcParams rcParams["figure.figsize"]= 12,6 rcParams["legend.loc"] = 'upper right' item_list = df.columns.tolist()[1:] colors = pd.DataFrame(y_pred).replace(0, "b").replace(1, "r").replace(2, "g") fig = plt.figure(1) ax = fig.add_subplot(111) index = 0 for item in item_list: plt.plot(df["time"], df[item], label = item+"_cluster"+str(y_pred[index]), color=colors[0][index]) index += 1 ax.set_xticklabels(df["time"], rotation = 45) plt.legend() plt.show()
ではDTWのk-meansを行います。
DTWのクラスタリングは時間が結構かかりました。
# DTW-k-means
from datetime import datetime
start_time = datetime.now()
print("DTW k-means")
dba_km = TimeSeriesKMeans(n_clusters=3,
n_init=2,
metric="dtw",
verbose=True,
max_iter_barycenter=10,
random_state=seed)
y_pred = dba_km.fit_predict(X_train.T)
print(y_pred)
end_time = datetime.now()
print('Duration: {}'.format(end_time - start_time))DTW k-means
Init 1
489.917 –> 172.116 –> 172.116 –>
Init 2
322.500 –> 163.240 –> 163.240 –>
[2 2 2 1 1 1 0 0 0 0 1 1]
Duration: 0:00:00.070831
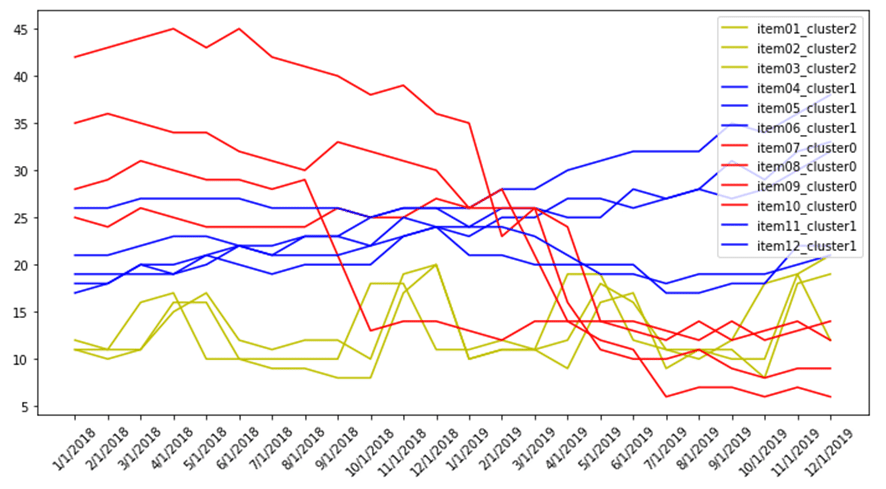
DTW k-meansのクラスタリングを可視化しました。
import matplotlib.pyplot as plt from pylab import rcParams rcParams["figure.figsize"]= 12,6 rcParams["legend.loc"] = 'upper right' item_list = df.columns.tolist()[1:] colors = pd.DataFrame(y_pred).replace(0, "r").replace(1, "b").replace(2, "g") fig = plt.figure(1) ax = fig.add_subplot(111) index = 0 for item in item_list: plt.plot(df["time"], df[item], label = item+"_cluster"+str(y_pred[index]), color=colors[0][index]) index += 1 ax.set_xticklabels(df["time"], rotation = 45) plt.legend() plt.show()
4. まとめ
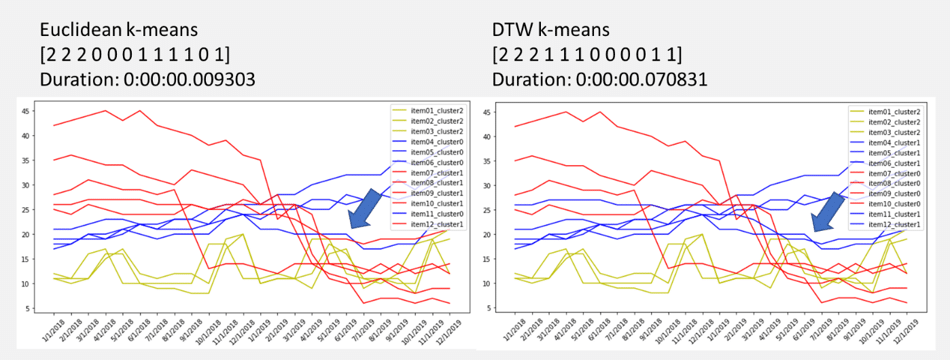
Euclidean と DTWの距離計算のk-meansを行いました。 両方の手法はクラスタリングができました。赤線のクラスターは頭が下がります。青い線のクラスターは上げる推移が続いてるまたは、横向きにしています。緑線のクラスターは季節的な横向きにしています。
Euclidean k-meansは赤線のクラスターは4つの線がありますが、青い線のクラスターは3つの線があります。 一方、DTWのk-meansは赤線のクラスターは3つの線がありますが、青い線のクラスターは4つの線があります。 また、Euclideanに対して、DTWの実行時間が結構かかりました。