前回の記事は回帰分析を説明しました。この記事では、回帰分析のお話になります。モデルを調整すると、精度よくなりますが、学習過ぎると過学習(Overfitting)になます。今回は過学習 / 未学習(Underfitting)を説明します。
過学習と
過学習とはoverfittingと呼ばれ、統計学や機械学習において、訓練データに対して学習されているが、未知データ(テストデータ)に対しては適合できていない、汎化できていない状態を指します。データが少ない時または、モデルが問題に対して複雑な時が原因だと考えられる事もあります。
未学習とは
未学習とはunderfittingと呼ばれ、訓練データから有用な特徴量を引き出して記憶することができず、やはり未知のデータへの予測性能は低くなってしまいます。
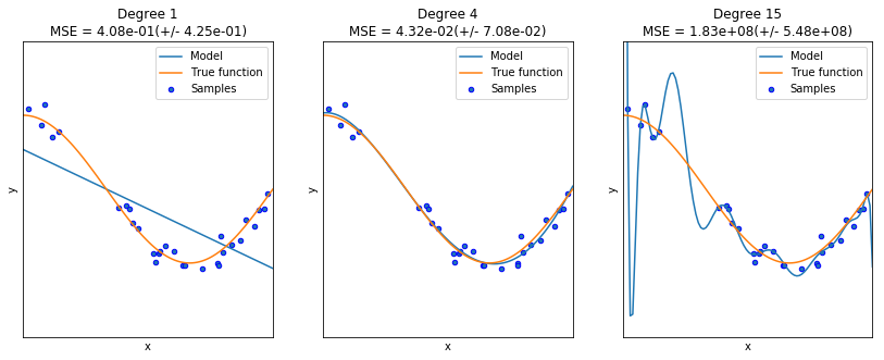
左の図は未学習です。線形モデルはトレーニングサンプルに適合するのに十分ではありません。 真ん中の図は、次数4の多項式は真の関数をほぼ完全に近似します。右の図は過学習で、モデルはトレーニングデータのノイズを学習してしまいました。
クロスバリデーションを使用して、オーバーフィッティング/アンダーフィッティングを確認することが出来ます。テストデータの平均二乗誤差(MSE)が低ければ、モデルの汎化性能(評価データへの適用能力)を正しく評価します。
Pythonのスクリプトの説明
# ライブラリーのインポート
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
# サンプルデータ作成
def true_fun(X):
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
degrees = [1, 4, 15]
# x y の加工
X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1
# 回帰分析
plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
polynomial_features = PolynomialFeatures(degree=degrees[i],
include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([(“polynomial_features”, polynomial_features),
(“linear_regression”, linear_regression)])
pipeline.fit(X[:, np.newaxis], y)
# cross validation
scores = cross_val_score(pipeline, X[:, np.newaxis], y,
scoring=”neg_mean_squared_error”, cv=10)
# 図作成
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label=”Model”)
plt.plot(X_test, true_fun(X_test), label=”True function”)
plt.scatter(X, y, edgecolor=’b’, s=20, label=”Samples”)
plt.xlabel(“x”)
plt.ylabel(“y”)
plt.xlim((0, 1))
plt.ylim((-2, 2))
plt.legend(loc=”best”)
plt.title(“Degree {}nMSE = {:.2e}(+/- {:.2e})”.format(
degrees[i], -scores.mean(), scores.std()))
plt.show()
Overfitting対策
1)サンプルサイズを増やす
サンプルのサイズは、収集できる情報の量に影響します。 詳細を知りたい場合は、サンプルサイズを大きくする必要があります。
2)関係ない変数を削除
あまりにも多くの変数がオーバーフィットの理由になります。 重要な変数のみを選択すると、過学習が抑えられ、テストデータの精度向上へ繋がります。
3)早期停止
学習アルゴリズムを繰り返し学習する場合、モデルの各反復がどれくらいうまく実行されるかを測定し、余り多く学習しないのも1つの手です。
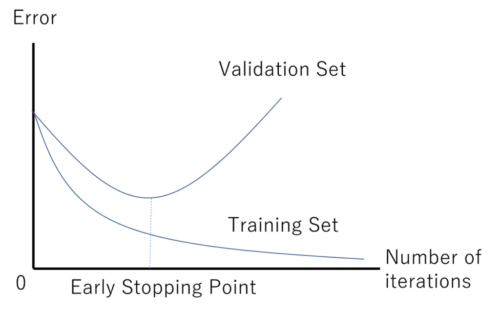
早期停止とは、学習をあるポイントを通過する前に中止することを指します。例えばですが、以下の図であれば、Validation setが最も小さいところで停止するのが過学習を抑える方法になります。
4)正規化
正規化とは、人為的にモデルを単純化するための幅広い手法を指します。
5)アンサンブル
アンサンブルは、複数の別々のモデルからの予測を結合する機械学習法です。
https://ja.wikipedia.org/wiki/%E9%81%8E%E5%89%B0%E9%81%A9%E5%90%88
http://scikit-learn.org/stable/auto_examples/model_selection/plot_underfitting_overfitting.html

Pingback: Keras AutoEncoder で異常検知「詐欺検知」 - S-Analysis