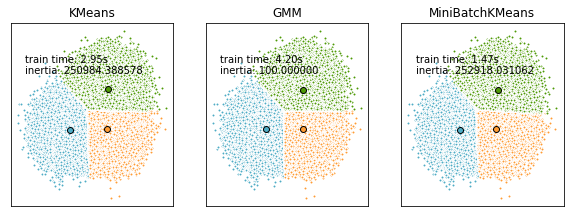
クラスタリング分析の話になっております。前回の記事にはGMMモデルについて話しました。GMMモデルのクラスタリングは計算時間がそれなりにかかりますので、大量のデータのプロジェクトには合わない事があります。その際にはMini Batch K-Means (ミニバッチ k平均)モデルを用いる事も1つの選択肢になります。
ミニバッチとは部分的にサンプリングされた入力データの一部です。これらのミニバッチでクラスタリングを行い、計算時間を大幅に短縮します。K-meansの結果と比べると若干悪い結果をもたらす事があります。
モデルの比較
Python Scriptの説明
<code>
# ライブラリの読み込み
print(__doc__)
import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GMM
from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets.samples_generator import make_blobs
# 300,000件のサンプルを作成する
np.random.seed(0)
batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]]
n_clusters = len(centers)
X, labels_true = make_blobs(n_samples=300000, centers=centers, cluster_std=0.7)
# K-Meanモデル学習を行う
k_means = KMeans(init=’k-means++’, n_clusters=3, n_init=10)
t0 = time.time()
k_means.fit(X)
t_batch = time.time() – t0
#GMM モデル学習を行う
t0 = time.time()
gmm = GMM(n_components=3).fit(X)
t_gmm = time.time() – t0
# K-Mean Mini Batchモデル学習を行う
mbk = MiniBatchKMeans(init=’k-means++’, n_clusters=3, batch_size=batch_size,
n_init=10, max_no_improvement=10, verbose=0)
t0 = time.time()
mbk.fit(X)
t_mini_batch = time.time() – t0
# 結果の図を作成する
fig = plt.figure(figsize=(8, 3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)
colors = [‘#4EACC5’, ‘#FF9C34’, ‘#4E9A06’]
# 結果の図を作成する
k_means_cluster_centers = np.sort(k_means.cluster_centers_, axis=0)
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)
gmm_cluster_centers = np.sort(gmm.means_, axis=0)
gmm_labels = pairwise_distances_argmin(X, gmm_cluster_centers)
mbk_means_cluster_centers = np.sort(mbk.cluster_centers_, axis=0)
mbk_means_labels = pairwise_distances_argmin(X, mbk_means_cluster_centers)
order = pairwise_distances_argmin(k_means_cluster_centers,
mbk_means_cluster_centers)
#K-Meansの図を作成する
ax = fig.add_subplot(1, 3, 1)
for k, col in zip(range(n_clusters), colors):
my_members = k_means_labels == k
cluster_center = k_means_cluster_centers[k]
ax.plot(X[my_members, 0], X[my_members, 1], ‘w’,
markerfacecolor=col, marker=’.’)
ax.plot(cluster_center[0], cluster_center[1], ‘o’, markerfacecolor=col,
markeredgecolor=’k’, markersize=6)
ax.set_title(‘KMeans’)
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, ‘train time: %.2fsninertia: %f’ % (
t_batch, k_means.inertia_))
#GMMの図を作成する
ax = fig.add_subplot(1, 3, 2)
for k, col in zip(range(n_clusters), colors):
my_members = gmm_labels == order[k]
cluster_center = gmm_cluster_centers[order[k]]
ax.plot(X[my_members, 0], X[my_members, 1], ‘w’,
markerfacecolor=col, marker=’.’)
ax.plot(cluster_center[0], cluster_center[1], ‘o’, markerfacecolor=col,
markeredgecolor=’k’, markersize=6)
ax.set_title(‘GMM’)
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, ‘train time: %.2fsninertia: %f’ %
(t_gmm, gmm.n_iter))
#K-Means Mini Batchの図を作成する
ax = fig.add_subplot(1, 3, 3)
for k, col in zip(range(n_clusters), colors):
my_members = mbk_means_labels == order[k]
cluster_center = mbk_means_cluster_centers[order[k]]
ax.plot(X[my_members, 0], X[my_members, 1], ‘w’,
markerfacecolor=col, marker=’.’)
ax.plot(cluster_center[0], cluster_center[1], ‘o’, markerfacecolor=col,
markeredgecolor=’k’, markersize=6)
ax.set_title(‘MiniBatchKMeans’)
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, ‘train time: %.2fsninertia: %f’ %
(t_mini_batch, mbk.inertia_))
plt.show()
</code>
