k-means++ – S-Analysis

前回の記事にはGMMモデルとMini Batch K-MeansとSpectral Clusteringについて説明します。この記事では、k-means++について説明していきます。

k-means++とは

k-means++法は、非階層型クラスタリング手法の1つで、k-means法の初期値の選択に改良を行なった方法です。

先ず、k-meansの初期値の流れは以下のようになります。

1. クラスタ数kを決める
2. データが含まれる空間にランダムにk個の点(セントロイド)を置く
3. 各データがセントロイドのうちどれに最も近いかを計算して、そのデータが所属するクラスタとする
4. セントロイドの位置をそのクラスタに含まれるデータの重心になるように移動する
（各セントロイドの重心が変わらなくなるまで3, 4を繰り返す）

k-meansのクラスタには、初期値が不適切であるときにうまく分類ができなかったりする問題も抱えています。下記のクラスタリングの結果は初期値（セントロイド）の問題について解決を図るためにk-means法の改良として考案されたのが，k-means++法です。

初期のクラスター中心をなるべく遠目におくという発想があります。まず始めにデータ点をランダムに選び1つ目のクラスタ中心とし、全てのデータ点とその最近傍のクラスタ中心の距離を求め、その距離の二乗に比例した確率でクラスタ中心として選ばれていないデータ点をクラスタ中心としてランダムに選んでいきます

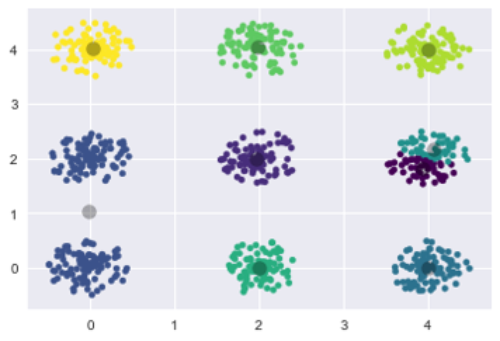
普通のk-meansでやると以下のような感じで見るからに無様な結果になっています．
これは初期セントロイドを乱数で割り当ててるために，近い位置にセントロイドが置かれた場合にこういう感じになってしまいます．

Python Scriptの説明

# ライブラリの読み込み

from sklearn.cluster import KMeans

import numpy as np

import matplotlib.pyplot as plt

#データロード

data = np.loadtxt('./data.txt', delimiter=' ')

#k-means++モデル作成

kmeans = KMeans(n_clusters=9, init='random', random_state=0)

y_kmeans = kmeans.fit_predict(data)

# グラフの作成

plt.scatter(data[:, 0], data[:, 1], c=y_kmeans, s=20, cmap='viridis')

centers = kmeans.cluster_centers_

plt.scatter(centers[:, 0], centers[:, 1], c='black', s=100, alpha=0.3);

kmeans_data はこちらです。

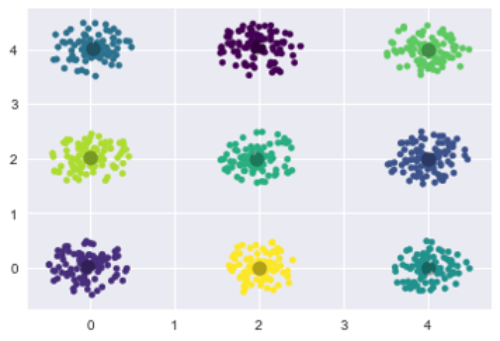
K-Means++結果

綺麗なクラスタリングになりました。このメリットは、初期値決めに余計な時間がかかるが、k-means法は収束がとても早く計算時間はそれほどかからない事です。著者らはこの手法を実データと人工データの両方で実験を行い、だいたい収束スピードに関しては2倍、あるデータセットでは誤差が1000分の1となったいう例もあります。

Python Scriptの説明

# ライブラリの読み込み

from sklearn.cluster import KMeans

import numpy as np

import matplotlib.pyplot as plt

#データロード

data = np.loadtxt(‘./data.txt’, delimiter=’ ‘)

#k-means++モデル作成

kmeans = KMeans(n_clusters=9, init=’k-means++’)

y_kmeans = kmeans.fit_predict(data)

# グラフの作成

plt.scatter(data[:, 0], data[:, 1], c=y_kmeans, s=20, cmap=’viridis’)

centers = kmeans.cluster_centers_

plt.scatter(centers[:, 0], centers[:, 1], c=’black’, s=100, alpha=0.3);

詳細な情報は以下をご覧ください

https://ja.wikipedia.org/wiki/K%E5%B9%B3%E5%9D%87%E6%B3%95

https://gist.github.com/Ooshita/afc4da3ae05fbff00dbb8a2ca8eb2bd2

http://tech.nitoyon.com/ja/blog/2013/11/07/k-means/

k-means++とは

K-Means++結果

2 thoughts on “k-means++”