前回の記事には クラスター分析 の手法について話しました。
今回の記事は、KNNでは分離が上手くいかない時に使用するクラスタリング手法として混合ガウス モデル (GMM)を紹介します。ただし計算時間はそれなりにかかります。
GMMはGaussian mixture modelsの略称です。GMM は”ソフト クラスタリング” 方式と見なすことができます。ソフトクラスタリング方式では、1つの点に対して複数のクラスに所属する確率を出す事ができます。
sklearn.mixture のパッケージでGMM の学習を行う例を以下に示します。混合正規分布の密度を計算し,可視化するスクリプトを作成しています.
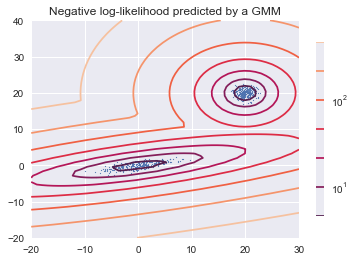
GMM による分類結果は図中の等高線で表現されます。 これは学習された混合正規分布の高さになります。例えば実際のデータでは、顧客分布で初見さんがやや多く、常連さんの山があるような場合に相当します。当然初見さんが多く、常連さんの山があるという見方ができます。
曲線の色はそれぞれの等高線ごとに分けています.以下では二つの分布になることがわかります。
Python Codeの説明
#ライブラリの読み込み
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from sklearn import mixture
#ランダムサンプル、2つの要素を作成する
n_samples = 300
# 地形データを作成 (20, 20)
shifted_gaussian = np.random.randn(n_samples, 2) + np.array([20, 20])
# Gaussianデータを作成する
C = np.array([[0., -0.7], [3.5, .7]])
stretched_gaussian = np.dot(np.random.randn(n_samples, 2), C)
# 2つのデータセットをトレーニングセットに連結する
X_train = np.vstack([shifted_gaussian, stretched_gaussian])
# GMMモデル学習を行う
clf = mixture.GaussianMixture(n_components=2, covariance_type=’full’)
clf.fit(X_train)
# モデルによる予測スコアを等高線図として表示する
x = np.linspace(-20., 30.)
y = np.linspace(-20., 40.)
X, Y = np.meshgrid(x, y)
XX = np.array([X.ravel(), Y.ravel()]).T
Z = -clf.score_samples(XX)
Z = Z.reshape(X.shape)
CS = plt.contour(X, Y, Z, norm=LogNorm(vmin=1.0, vmax=1000.0),
levels=np.logspace(0, 3, 10))
CB = plt.colorbar(CS, shrink=0.8, extend=’both’)
plt.scatter(X_train[:, 0], X_train[:, 1], .8)
plt.title(‘Negative log-likelihood predicted by a GMM’)
plt.axis(‘tight’)
plt.show()
Covariance Typeのパラメーター設定
Covariance typeのオプションはspherical, tied, diag, fullがあります。Covariance typeはクラスターの形を設定し、チューニングが必要です。それぞれの意味は以下になります。
‘spherical’(各構成要素には独自の分散があります)。
‘tied’(すべての構成要素が同じ一般的な共分散行列を共有する)
‘diag’(各構成要素には独自の対角共分散行列があります)
‘full’(各構成要素には独自の一般共分散行列があります)
Irisデータセットの各Covariance typeの学習を行う例を以下に示します。
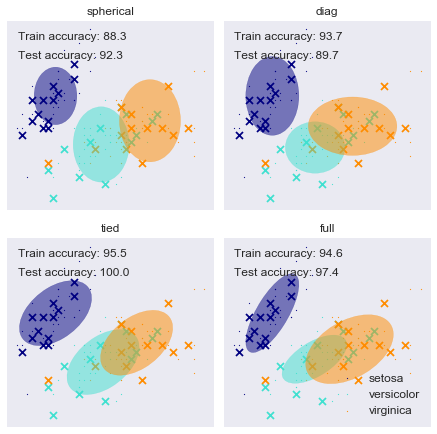
左上の青い部分は、どのクラスターでも上手くわかれていますが、それなりに混ざったものがある場合は、分類がそれなりに間違えています。テストで評価するのならばtiedが一番よいように見えますが、学習が悪くバランスが悪いように見えます。このときモデルを選択する方法としてBICの値を比較する方法があります。以下になります。
最適なモデル
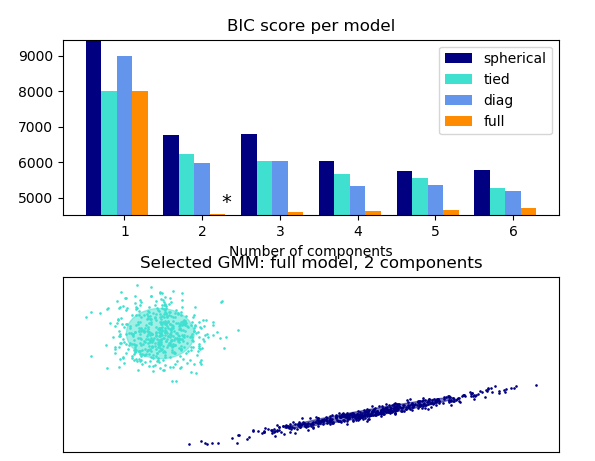
GMMモデルのパラメーターの比較のために、BICスコアを計算します。一番良いモデルは、2つの要素で’full’のモデルです(BICスコアが最も低いものを選びます)。クラスター数2で
十分値が小さくなっているので2つの要素に分割を選びます。
Python Codeの説明
# ライブラリの読み込み
import numpy as np
import itertools
from scipy import linalg
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import mixture
print(__doc__)
#ランダムサンプル、2つの要素を作成する
n_samples = 500
np.random.seed(0)
C = np.array([[0., -0.1], [1.7, .4]])
X = np.r_[np.dot(np.random.randn(n_samples, 2), C),
.7 * np.random.randn(n_samples, 2) + np.array([-6, 3])]
lowest_bic = np.infty
bic = []
n_components_range = range(1, 7)
cv_types = [‘spherical’, ‘tied’, ‘diag’, ‘full’]
for cv_type in cv_types:
for n_components in n_components_range:
# Fit a Gaussian mixture with EM
gmm = mixture.GaussianMixture(n_components=n_components,
covariance_type=cv_type)
gmm.fit(X)
bic.append(gmm.bic(X))
if bic[-1] < lowest_bic:
lowest_bic = bic[-1]
best_gmm = gmm
bic = np.array(bic)
color_iter = itertools.cycle([‘navy’, ‘turquoise’, ‘cornflowerblue’,
‘darkorange’])clf = best_gmm
bars = []
# BICスコアの図を作成する
spl = plt.subplot(2, 1, 1)
for i, (cv_type, color) in enumerate(zip(cv_types, color_iter)):
xpos = np.array(n_components_range) + .2 * (i – 2)
bars.append(plt.bar(xpos, bic[i * len(n_components_range):
(i + 1) * len(n_components_range)],
width=.2, color=color))
plt.xticks(n_components_range)
plt.ylim([bic.min() * 1.01 – .01 * bic.max(), bic.max()])
plt.title(‘BIC score per model’)
xpos = np.mod(bic.argmin(), len(n_components_range)) + .65 +
.2 * np.floor(bic.argmin() / len(n_components_range))
plt.text(xpos, bic.min() * 0.97 + .03 * bic.max(), ‘*’, fontsize=14)
spl.set_xlabel(‘Number of components’)
spl.legend([b[0] for b in bars], cv_types)
# 一番よいBICスコアのモデル図を作成する
splot = plt.subplot(2, 1, 2)
Y_ = clf.predict(X)
for i, (mean, cov, color) in enumerate(zip(clf.means_, clf.covariances_,
color_iter)):
v, w = linalg.eigh(cov)
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color)
# Plot an ellipse to show the Gaussian component
angle = np.arctan2(w[0][1], w[0][0])
angle = 180. * angle / np.pi # convert to degrees
v = 2. * np.sqrt(2.) * np.sqrt(v)
ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(.5)
splot.add_artist(ell)
plt.xticks(())
plt.yticks(())
plt.title(‘Selected GMM: full model, 2 components’)
plt.subplots_adjust(hspace=.35, bottom=.02)
plt.show()
