【ROC曲線とAUC】機械学習の評価指標

機械学習のモデル作成後にテストデータを使って「本当に良いモデルなのか？」という評価を必ず行う必要があります。今回の記事は分類問題に対して評価指標のROC曲線とAUCについて説明します。他にも評価指標は色々とあるので、随時記事にしていく予定です。

AUCとは

AUCとは、二値分類器の評価指標として Area Under the ROC Curve の略です。サンプルに対して 0から1の範囲でスコア（確率）を与える二値分類器の精度を評価することを考えています。予測スコアでサンプルを（降順）ソートしたときに、真値のTrue となるサンプルが真値のFalse となるサンプルより上位にきているか』ということを測っています。つまり、ラベル 1 のサンプルに正しく高スコアを与える予測器であるかを見ています。

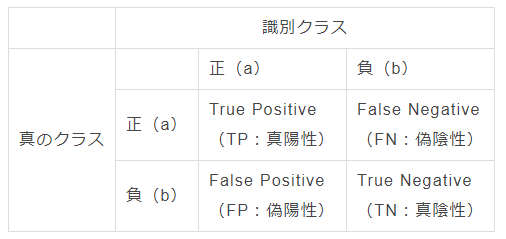
縦軸がモデルの予測で、横軸が正解データになります。

各象限の説明を簡単にすると、

True Positive(TP)：正解データ正であるものを、正しく正と予測できた数
False Positive(FP)：正解データ負であるものを、間違って正と予測した数
Flase Negative(FN)：正解データ正であるものを、間違って負と予測した数
True Negative(TN)：正解データ負であるものを、正しく負と予測できた数

ROC曲線をプロット

先程の偽陽性率と真陽性率の表をプロットすると以下のようなグラフが出来上がります。このように、閾値を変化させたときの偽陽性率と真陽性率による各点を結んだものがROC曲線です。

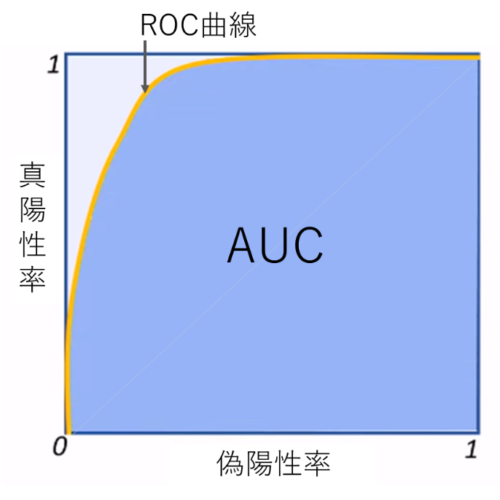
閾値を移動させながらPositive / Negativeを判別していくことを考えます。そうすると閾値が0のときは全てNegativeに判断するので偽陽性は0になります。ここから閾値を増加させていくと偽陽性と真陽性が増加していきます。そして閾値が1となったとき全てPositiveと判断するので偽陽性は1になります。モデルの識別能力が高ければ左上に凸のグラフになりますが、識別能力が低ければグラフは対角線上に近づきます。

Sklearnのpython

# ライブラリーのインポート

import numpy as np

import matplotlib.pyplot as plt

from sklearn import svm, datasets

from sklearn.metrics import roc_curve, auc

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import label_binarize

from sklearn.multiclass import OneVsRestClassifier

# irisデータロード

iris = datasets.load_iris()

X = iris.data

y = iris.target

# バイナリデータの変更

y = label_binarize(y, classes=[0, 1, 2])

n_classes = y.shape[1]

# ノイズの追加

random_state = np.random.RandomState(0)

n_samples, n_features = X.shape

X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]

# 学習・テストの分割

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=0)

# 分類モデル

classifier = OneVsRestClassifier(svm.SVC(kernel=’linear’, probability=True,

random_state=random_state))

y_score = classifier.fit(X_train, y_train).decision_function(X_test)

# ROC曲線計算

fpr = dict()

tpr = dict()

roc_auc = dict()

for i in range(n_classes):

fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])

roc_auc[i] = auc(fpr[i], tpr[i])

fpr[“micro”], tpr[“micro”], _ = roc_curve(y_test.ravel(), y_score.ravel())

roc_auc[“micro”] = auc(fpr[“micro”], tpr[“micro”])

#ROC図作成

plt.figure()

lw = 2

plt.plot(fpr[2], tpr[2], color=’red’,

lw=lw, label=’ROC curve (area = %0.2f)’ % roc_auc[2])

plt.plot([0, 1], [0, 1], color=’navy’, lw=lw, linestyle=’–‘)

plt.xlim([0.0, 1.0])

plt.ylim([0.0, 1.05])

plt.xlabel(‘False Positive Rate’)

plt.ylabel(‘True Positive Rate’)

plt.title(‘Receiver operating characteristic’)

plt.legend(loc=”lower right”)

plt.show()

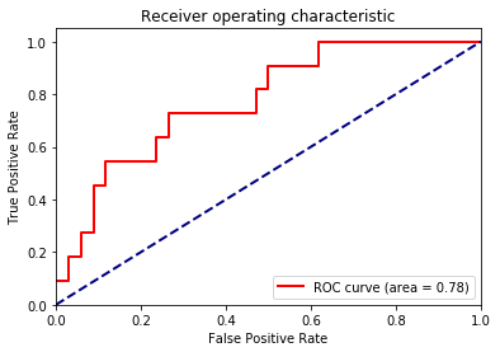
斜め45度の線よりも高い事からこのモデルを使うとランダムでやったときよりも効果があるという事がわかります。また複数のモデルの比較においてもAUCスコアが高いものを採用する事でモデル比較が出来ます。

http://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.html#sphx-glr-auto-examples-model-selection-plot-roc-py

AUCとは

2 thoughts on “【ROC曲線とAUC】機械学習の評価指標”