最近、ニュースや記事でよく目にする、耳にする“ ディープラーニング(Deep Learning) ” 。ディープラーニングに興味ある方が多方面に増えてきている一方で、Deep Learningについて知りたいけれども、実際よくわからないと感じている方も多く見受けられます。この記事はディープラーニングについて説明します。過去に紹介してきたクラスタリングや回帰分析とは異なります。
ディープラーニングとは
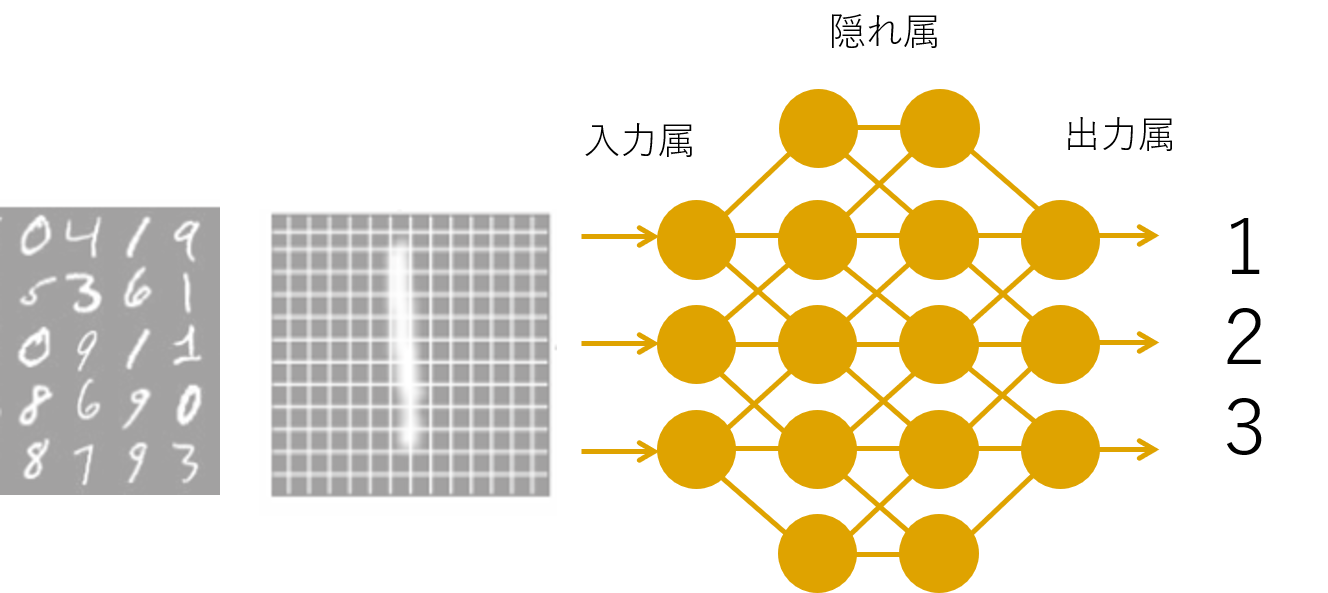
ディープラーニング(deep learning)または深層学習とは、人間の脳神経回路を模したニューラルネットワークを多層的にすることで、コンピューター自らがデータに含まれる潜在的な特徴をとらえ、より正確で効率的な判断を実現させる技術や手法です。
具体的な例は、世界囲碁トップレベルに勝利した人工知能の囲碁プログラム「AlphaGo」のアルゴリズムはディープラーニングです。
「機械学習」と「ディープラーニング」の違いとは?
ディープラーニングは機械学習をさらに発展させたものだ。従来の機械学習との大きな違いは、情報やデータを分析する際に使う枠組みが異なっていること。構成、データ量、コンピューティングソースなどの異は下記の表にまとめました。

実験
ディープラーニングを実験すると思っていたところ、kerasでmnistのデータを画像分類します。
Kerasは,Pythonで書かれた,TensorFlowまたはCNTK,Theano上で実行可能な高水準のニューラルネットワークライブラリです. Kerasは,コードが書きやすく、迅速な実験を可能にすることに重点を置いて開発されました. アイデアから結果を得るまでの時間を早くする事で試行錯誤をしやすいというメリットがあります。
mnistのデータ
28×28ピクセル、白黒画像の 手書き数字 のデータセットになります。各ピクセルは0(白)~255(黒)の値をとる。6万枚の学習用画像と1万枚のテスト画像が入っています。今回は活性化関数を変えながら精度と時間比較をしてみます。
https://keras.io/ja/datasets/#mnist
実行環境
Python3.6
Anaconda 5.2.0
Jupyter Notebook5.6.0
Python ライブラリー
- Tensoflow 1.10.0
- Keras 2.2.2
- Sklearn 0.19.1
mnist_kerasのPython
import numpy as np
import tensorflow as tf
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.optimizers import SGD
from sklearn import datasets
from sklearn.model_selection import train_test_split
from tensorflow.examples.tutorials.mnist import input_data
%matplotlib inline
import matplotlib.pyplot as plt
tf.logging.set_verbosity(tf.logging.ERROR)
n = len(mnist.train.images)
N = 10000 # MNISTの一部を使う
indices = np.random.permutation(range(n))[:N] # ランダムにN枚を選択
X = mnist.train.images[indices]
y = mnist.train.labels[indices]
# 0枚目の画像は ‘0’ を表す
print(X_train[0])
print(X_train[0])
plt.imshow(X_train[0].reshape((28, 28)), cmap=’gray’)
n_in = len(X[0]) # 784
n_hidden = 200
n_out = len(y[0]) # 10
alpha = 0.01
model = Sequential()
model.add(Dense(n_hidden, input_dim=n_in))
# relu / tanh / sigmoid /elu
# 詳しくはhttps://keras.io/ja/activations/
model.add(Activation(‘sigmoid’))
model.add(Dense(n_hidden))
#model.add(Activation(‘sigmoid’))
#model.add(Dense(n_hidden))
#model.add(Activation(‘sigmoid’))
#model.add(Dense(n_hidden))
model.add(Dense(n_out))
model.add(Activation(‘softmax’))
model.compile(loss=’categorical_crossentropy’,
optimizer=SGD(lr=0.01),
metrics=[‘accuracy’])
epochs = 100
batch_size = 200
model.fit(X_train, Y_train, epochs=epochs, batch_size=batch_size)
loss_and_metrics = model.evaluate(X_test, Y_test)
print(loss_and_metrics)
結果
活性化関数を変えてみて、relu, tanh, sigmoid, eluのパラメーターでの結果を比較しました。reluは精度が一番高いのがわかります。またelu関数だと速度が最もワンステップ辺り早い事もわかります。
Activation(‘relu’)
Rectified Linear Unit
1s 65us/step – loss: 0.1025 – acc: 0.9761
(Activation(‘tanh’)
Hyperbolic tangent activation function
1s 79us/step – loss: 0.1610 – acc: 0.9568
Activation(‘sigmoid’)
Sigmoid activation function
1s 65us/step – loss: 0.2866 – acc: 0.9146
(Activation(‘elu’)
Exponential linear unit
1s 63us/step – loss: 0.1741 – acc: 0.9563
