Networkxのネットワーク類似度

1. NetworkXの概要

NetworkXは、グラフ/ネットワークの作成、加工、構造分析をのPythonのパッケージです。そもそも、数学者、物理学者、生物学者、コンピューター科学者、社会科学者などの分野で活用されています。ソーシャルネットワーク、分子グラフ、通信ネットワーク、物流ネットワーク、エネルギーネットワークなどの分析を対応します。

このライブラリは多くの機能があり、今回はネットワーク類似度を解説します。

2. NetworkXの類似性の測定（編集距離）

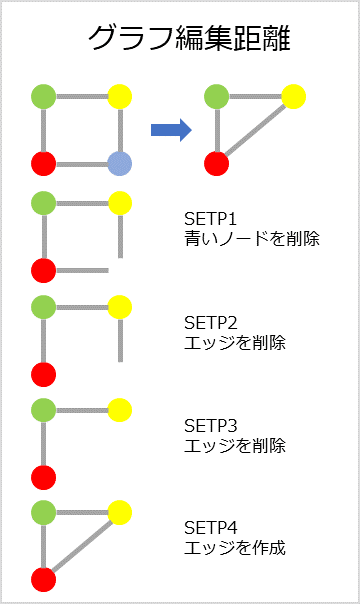
グラフ編集距離は、2つのグラフを同形にするために必要なエッジ/ノードの変更の数です。

デフォルトのアルゴリズムは、正確な値ではなく近似値を用いています。理由は、正確なグラフ編集距離（Graph Edit Distance – GED）における計算の問題は、多くの場合時間がかかります。

グラフ編集距離の例

四角のグラフは三角のグラフに編集は以下の図のような4つステップです。この時は、距離４です。

NetworkXのsimilarityのモジュール：

graph_edit_distance(G1, G2[, node_match, …])	グラフG1とG2の間のGED（グラフ編集距離）を返します。
optimal_edit_paths(G1, G2[, node_match, …])	G1をG2に変換するすべての最小コストの編集パスを返します。
optimize_graph_edit_distance(G1, G2[, …])	グラフG1とG2の間のGED（グラフ編集距離）の連続近似を返します。
optimize_edit_paths(G1, G2[, node_match, …])	GED (graph edit distance) calculation: advanced interface.
simrank_similarity(G[, source, target, …])	GED（グラフ編集距離）計算：高度なインターフェイス。
simrank_similarity_numpy(G[, source, …])	numpyの行列を使用して、GのノードのSimRankを計算します。

3. 実験

環境：Google Colab（Colaboratory）

データ：生成したデータ

分析：ネットワークのネットワーク類似度

Colab ではnetworkx をインストールしています。ローカル環境などにインストールする場合は、下記のコードを実行してください。

pip install networkx

ライブラリのインポート

import numpy as np

import networkx as nx

import matplotlib.pyplot as plt

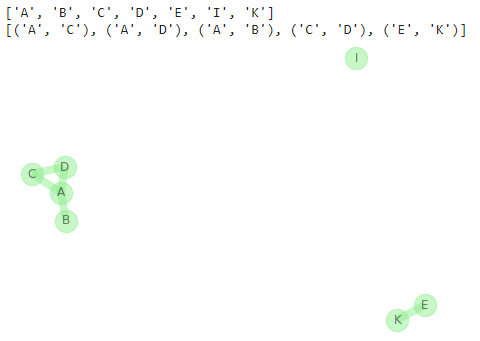
ネットワークG1を作成します。

G1 = nx.Graph()

G1.add_nodes_from([(‘A’, {‘label’:’S1′}),

(‘B’, {‘label’:’S1′}),

(‘C’, {‘label’:’S1′}),

(‘D’, {‘label’:’S1′}),

(‘E’, {‘label’:’S2′}),

(‘I’, {‘label’:’S2′}),

(‘K’, {‘label’:’S2′})])

G1.add_edges_from([(‘A’,’C’), (‘A’, ‘D’),

(‘K’, ‘E’), (‘D’, ‘A’),

(‘A’, ‘B’), (‘C’, ‘D’)])

print(G1.nodes())

print(G1.edges())

nx.draw(G1,

node_color=’lightgreen’,

edge_color=’lightgreen’,

node_size=500,

width=8,

alpha=0.5,

with_labels=True)

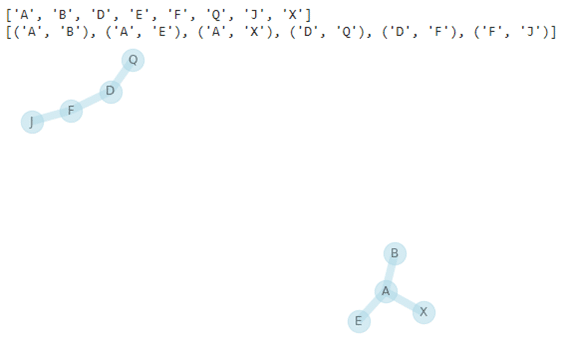
ネットワークG2を作成します。

G2 = nx.Graph()

G2.add_nodes_from([(‘A’, {‘label’:’S1′}),

(‘B’, {‘label’:’S1′}),

(‘D’, {‘label’:’S1′}),

(‘E’, {‘label’:’S1′}),

(‘F’, {‘label’:’S2′}),

(‘Q’, {‘label’:’S2′}),

(‘J’, {‘label’:’S2′}),

(‘X’, {‘label’:’S2′})])

G2.add_edges_from([(‘A’,’B’), (‘Q’, ‘D’),

(‘J’,’F’), (‘A’, ‘E’),

(‘D’, ‘F’), (‘X’,’A’)])

print(G2.nodes())

print(G2.edges())

nx.draw(G2,

node_color=’lightblue’,

edge_color=’lightblue’,

node_size=500,

width=8,

alpha=0.5,

with_labels=True)

G1とG2を集合します。

G12 = nx.compose(G1,G2)

print(‘G1 count:’, len(G1))

print(‘G2 count:’, len(G2))

print(‘G1・G2 compose:’, len(G12))

print(G12.nodes())

G1 count: 7

G2 count: 8

G1・G2 compose: 11

[‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘I’, ‘K’, ‘F’, ‘Q’, ‘J’, ‘X’]

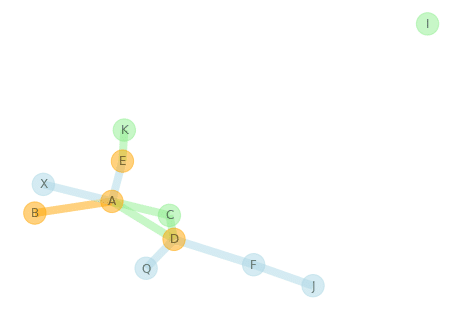
共通部分のノードとエッジの可視化

G1は緑色、G2は水色、共通部分はオレンジ色です。

# set edge colors

edge_colors = dict()

for edge in G12.edges():

if G1.has_edge(*edge):

if G2.has_edge(*edge):

edge_colors[edge] = ‘orange’

continue

edge_colors[edge] = ‘lightgreen’

elif G2.has_edge(*edge):

edge_colors[edge] = ‘lightblue’

# set node colors

G1_nodes = set(G1.nodes())

G2_nodes = set(G2.nodes())

node_colors = []

for node in G12.nodes():

if node in G1_nodes:

if node in G2_nodes:

node_colors.append(‘orange’)

continue

node_colors.append(‘lightgreen’)

if node in G2_nodes:

node_colors.append(‘lightblue’)

pos = nx.spring_layout(G12, scale=10)

nx.draw(G12, pos,

nodelist=G12.nodes(),

node_color=node_colors,

edgelist=edge_colors.keys(),

edge_color=edge_colors.values(),

node_size=500,

width=8,alpha=0.5,

with_labels=True)

Jaccard係数

Jaccard係数の集合の類似度を計算します。

def jaccard_similarity(G1, G2):

i = set(G1).intersection(G2)

return round(len(i) / (len(G1) + len(G2) – len(i)),3)

jaccard_similarity(G1.edges(), G2.edges())

0.1

graph_edit_distance

G1とG2の間のGED（グラフ編集距離）を計算します。

nx.graph_edit_distance(G1, G2)

4.0

optimal_edit_paths

G1をG2に変換するすべての最小コストの編集パスを返します。

nx.optimal_edit_paths(G1, G2)

([([(‘B’, ‘X’),

(‘E’, ‘J’),

(‘I’, ‘Q’),

(‘K’, ‘F’),

(‘C’, ‘E’),

(None, ‘D’),

(‘D’, ‘B’),

(‘A’, ‘A’)],

…

[((‘C’, ‘D’), (‘F’, ‘J’)),

((‘A’, ‘C’), (‘D’, ‘F’)),

((‘A’, ‘D’), None),

((‘A’, ‘B’), (‘D’, ‘Q’)),

((‘E’, ‘K’), (‘A’, ‘E’)),

(None, (‘A’, ‘B’)),

(None, (‘A’, ‘X’))])],

4.0)

optimize_graph_edit_distance

G1とG2の間のGED（グラフ編集距離）の連続近似を返します。

for dist in nx.optimize_graph_edit_distance(G1, G2, node_match=lambda a,b: a[‘label’] == b[‘label’]):

print(dist)

13.0

11.0

simrank_similarity

GED（グラフ編集距離）計算します。

# simrank_similarity

sim = nx.simrank_similarity(G1)

lol = [[sim[u][v] for v in sorted(sim[u])] for u in sorted(sim)]

sim_array = np.array(lol)

print(sim_array)

[[1. 0.53680108 0.62626793 0.62626793 0. 0. 0. 0. ]

[0.53680108 1. 0.73182057 0.73182057 0. 0. 0. 0. ]

[0.62626793 0.73182057 1. 0.65396202 0. 0. 0. 0. ]

[0.62626793 0.73182057 0.65396202 1. 0. 0. 0. 0. ]

[0. 0. 0. 0. 1. 0. 0. 0. ]

[0. 0. 0. 0. 0. 1. 0. 0. ]

[0. 0. 0. 0. 0. 0. 1. 0. ]

[0. 0. 0. 0. 0. 0. 0. 1. ]]

担当者：KW
バンコクのタイ出身　データサイエンティスト
製造、マーケティング、財務、AI研究などの様々な業界にPSI生産管理、在庫予測・最適化分析、顧客ロイヤルティ分析、センチメント分析、SaaS、PaaS、IaaS、AI at the Edge の環境構築などのスペシャリスト

目次

1. NetworkXの概要

2. NetworkXの類似性の測定（編集距離）

3. 実験

ライブラリのインポート

共通部分のノードとエッジの可視化

Jaccard係数

graph_edit_distance

optimal_edit_paths

optimize_graph_edit_distance

simrank_similarity