線形判別分析(Linear Discriminant Analysis) LDA 次元削減

1. 線形判別分析 (LDA) とは

線形判別分析（Linear Discriminant Analysis, LDA）は、次元削減を用いた統計学上の特徴抽出手法のひとつです。主成分分析 (Principle Component Analysis, PCA) は、データの分散が最大となるような次元を探すのに対して、線形判別分析は、データのクラスを最もよく分けられる次元を探します。ここでは、主成分分析 (PCA)と線形判別分析 (LDA)を比較していきたいと思います。

線形判別分析の手法
グループ間の分散を最大にグループの分類を最小にする軸を選びます。
1. クラス内およびクラス間の散布行列を計算します。
2. 散布行列の固有ベクトルと対応する固有値を計算します。
3. 固有値を並べ替えて、上位kを選択します。
4. k個の固有値にマップする固有ベクトルを含む新しい行列を作成します。
5. ステップ4のデータと行列の内積を取得して、新しい特徴（つまり、LDAコンポーネント）を取得します。

線形判別分析の特徴：
・分離を最適化する特徴部分空間を探す
・教師あり
・正規分布が仮定される
・サンプル間が独立であることが仮定される

scikit learnの線形判別分析

sklearn.discriminant_analysis.LinearDiscriminantAnalysis(*, solver=’svd’, shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001)

パラメター
solver{‘svd’, ‘lsqr’, ‘eigen’}, default=’svd
学習の最適化計算のタイプ

shrinkage‘auto’ or float, default=None
学習データの不足補正。”lsqr”, “eigen”で使われます。

priorsarray-like of shape (n_classes,), default=None
クラスの事前確率

n_componentsint, default=None
削減する次元数

store_covariancebool, default=False
共分散行列を計算するかどうか

tolfloat, default=1.0e-4
特異値の絶対しきい値（SDVのしきい値）

2. 実験

環境：Google Colab
データセット：ペンギンのデータセット
データセットには、344羽のペンギンのデータが含まれています。このデータセットには、南極のパルマー諸島の3つの島から収集された、3種類のペンギンがいます。特徴量はペンギン嘴（くちばし）の長さと深さ・体重・性別になります。

https://github.com/allisonhorst/palmerpenguins

モデル：主成分分析 (PCA)と線形判別分析 (LDA)
https://scikit-learn.org/stable/modules/generated/sklearn.discriminant_analysis.LinearDiscriminantAnalysis.html

ライブラリインポート

import numpy as np
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

sns.set(style='white', context='notebook', rc={'figure.figsize':(14,10)})

2.1 データロード

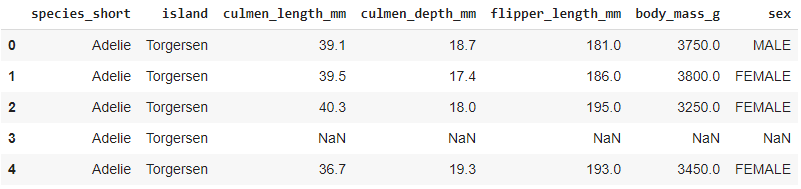
データフレーム作成します。

# データロード

penguins = pd.read_csv("https://github.com/allisonhorst/palmerpenguins/raw/5b5891f01b52ae26ad8cb9755ec93672f49328a8/data/penguins_size.csv")
penguins.head()

2.2 データ前処理

モデル作成のために、カテゴリデータを数値データに変換します。

# Category to Numeric Transformation

species_short_map = {'species_short': {'Adelie': 0, 'Chinstrap': 1, 'Gentoo': 2}}
penguins.replace(species_short_map, inplace=True)
penguins['species_short'] = penguins['species_short'].astype(float)

island_map = {'island': {'Biscoe': 0, 'Dream': 1, 'Torgersen': 2}}
penguins.replace(island_map, inplace=True)
penguins['island'] = penguins['island'].astype(float)

penguins['sex'] = penguins['sex'].map({'MALE': 0,'FEMALE': 1})

print(species_short_map)
print(island_map)

{‘species_short’: {‘Adelie’: 0, ‘Chinstrap’: 1, ‘Gentoo’: 2}}
{‘island’: {‘Biscoe’: 0, ‘Dream’: 1, ‘Torgersen’: 2}}

データ種類を確認します。

penguins.info()

<class ‘pandas.core.frame.DataFrame’>
RangeIndex: 344 entries, 0 to 343
Data columns (total 7 columns):
# Column Non-Null Count Dtype
— —— ————– —–
0 species_short 344 non-null float64
1 island 344 non-null float64
2 culmen_length_mm 342 non-null float64
3 culmen_depth_mm 342 non-null float64
4 flipper_length_mm 342 non-null float64
5 body_mass_g 342 non-null float64
6 sex 333 non-null float64
dtypes: float64(7)
memory usage: 18.9 KB

欠損値を確認します。

# Count Null

print('Total Null', penguins.isnull().values.sum())
print(penguins.isnull().sum())

Total Null 19
species_short 0
island 0
culmen_length_mm 2
culmen_depth_mm 2
flipper_length_mm 2
body_mass_g 2
sex 11
dtype: int64

欠損値を削除します。

# Drop Null

penguins = penguins.dropna()
print('Total Null', penguins.isnull().values.sum())

ペアプロット図（散布図行列）を作成します。

sns.pairplot(penguins, hue='species_short')

説明変数と目的変数を作成します。

X = penguins.drop(['species_short'], axis=1).to_numpy()
y = penguins['species_short'].to_numpy()
target_names = ['Adelie', 'Chinstrap', 'Gentoo']

print(X.shape)
print(y.shape)
print(target_names)

(333, 6)
(333,)
[‘Adelie’, ‘Chinstrap’, ‘Gentoo’]

Scikit-learnのデータのスケールでデータを標準化します。

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()
X = sc.fit_transform(X)

2.3 主成分分析 (PCA)

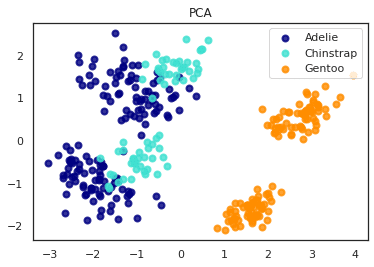
主成分分析を行いました。AdelieとChinstrapのペンギンは似ていると分かりました。

# 主成分分析 (PCA)

pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)

print('explained variance ratio (first two components): %s'
% str(pca.explained_variance_ratio_))

plt.figure()
colors = ['navy', 'turquoise', 'darkorange']
lw = 2

for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw,
label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA')

plt.show()

2.4 線形判別分析 (LDA)

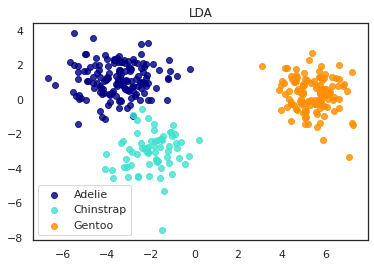
線形判別分析も同じ結果で、AdelieとChinstrapのペンギンは似ている事がわかります。

# 線形判別分析 (LDA) 
lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)

# Percentage of variance explained for each components
print('explained variance ratio (first two components): %s'
% str(pca.explained_variance_ratio_))

plt.figure()
colors = ['navy', 'turquoise', 'darkorange']
lw = 2

plt.figure()
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_r2[y == i, 0], X_r2[y == i, 1], alpha=.8, color=color,
label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA')

plt.show()

担当者：KW
バンコクのタイ出身　データサイエンティスト
製造、マーケティング、財務、AI研究などの様々な業界にPSI生産管理、在庫予測・最適化分析、顧客ロイヤルティ分析、センチメント分析、SaaS、PaaS、IaaS、AI at the Edge の環境構築などのスペシャリスト

目次