生存分析のKaplan-Meier

1. 生存分析の概要

生存分析とは、
生存分析は何らかのイベントが起きるまでの時間とイベント発生率の統計的手法です。イベントは、死、回復、誕生、退職のような目的変数です。

どのような分析：
・患者が症状を示すまでの日数を見つけること
・複数のグループ間のイベントを比較すること
・どの治療法が最も高い生存確率があるかを見つけること
・患者の生存数の中央値を見つけること
・どの要因が患者の生存により大きな影響を与えるかを比較すること

生存時間とは、被験者が生きているか、または積極的に調査期間に参加するまでの時間のことです。

イベントの主な種類：
1) 再発（Relapse: relapse-free survival）：治療後、元気になるまでの時間。
2)プログレッション（Progression: progression-free survival）：治療後、まだ病気で生きているが悪化しない時間。
3) 死(Death)：破壊または研究の永久的な終了です。
打ち切り(Censoring) は、データの欠落の問題の一種であり、何らかの理由でイベントまでの時間が観察されません。

2. 使用事例

医療
・患者の生存時間分析
・治療時間分析
製造
・機械故障時間分析
・運用生産障害分析
・機械のクリティカルレベル
・修理期間分析
ビジネス
・保証請求期間の分析
・販売時間分析につながる
・最初の販売分析に販売員の分析

3. 実験

環境：Google Colab
ライブラリ：lifelines
lifelinesは、純粋なPythonで記述された完全な生存分析ライブラリです。ライフラインライブラリーは以下のメリットがあります。

・簡単インストール
・内部プロット方法
・シンプルで直感的なAPI
・右、左、間隔の打ち切りデータを処理します
・最も人気のあるパラメトリック、セミパラメトリック、および非パラメトリックモデルが含まれる

詳細：https://lifelines.readthedocs.io/en/latest/

データセット：NCCTG Lung Cancer Data
North Central Cancer Treatment Groupの進行性肺癌患者の生存率。パフォーマンススコアは、患者が通常の日常活動をどのような生活をおくれるのかを評価します。
詳細：http://www-eio.upc.edu/~pau/cms/rdata/doc/survival/lung.html

3.1 Kaplan-Meier

ライブラリのインストール

!pip install lifelines

ライブラリのインポート

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import urllib
from urllib import request
import lifelines
from lifelines import KaplanMeierFitter

print('lifelines version: ', lifelines.__version__)

lifelines version: 0.25.5

データダウンロード

# Download data
csv_src = "http://www-eio.upc.edu/~pau/cms/rdata/csv/survival/lung.csv"
csv_path = 'lung.csv'
urllib.request.urlretrieve(csv_src, csv_path)

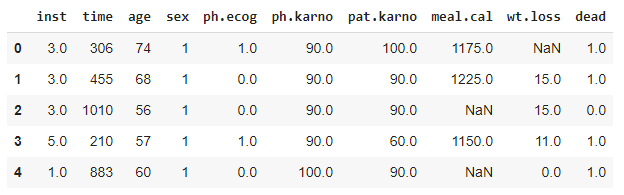
データフレーム作成

# Create dataframe

df = pd.read_csv(csv_path)
# Precessing
df.loc[df.status == 1, 'dead'] = 0
df.loc[df.status == 2, 'dead'] = 1
df = df.drop(['Unnamed: 0', 'status'], axis=1)
df.head()

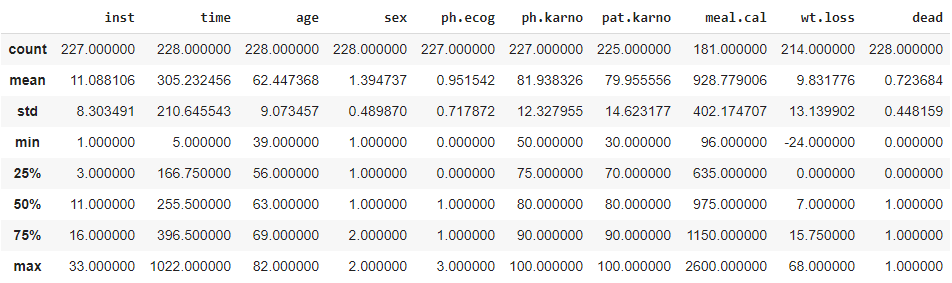
# Get statistical info
df.describe()

Kaplan-Meier-Fitterの実行

# Kaplan-Meier-Fitter
kmf = KaplanMeierFitter()
kmf.fit(durations = df.time, event_observed = df.dead)

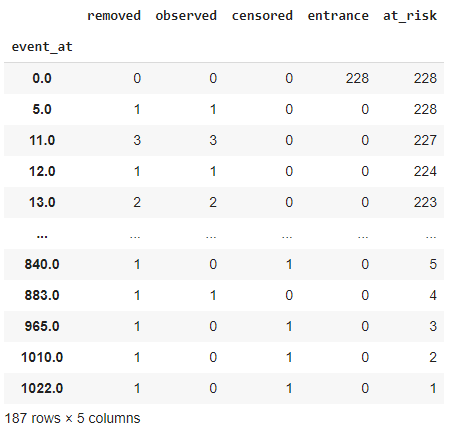
イベントテーブルを表示
event_at：データセットのタイムライン
removed：実験の一部ではなくなった被験者の値
observed：実験中に死亡した被験者の数の値
censored：観察時間中にイベントが発生していない被験者の数
entrance：特定のタイムラインにおける新しい主題の価値
at_risk：現在監視中の被験者の数。

kmf.event_table

生存率の計算
生存率　=（開始時にリスクのある被験者の数 – 死亡した被験者の数）/開始時にリスクのある被験者の数。

# Calculate survival probability for given time
print("Survival probablity for t=0: ", kmf.predict(0))
print("Survival probablity for t=5: ", kmf.predict(5))
print("Survival probablity for t=11: ", kmf.predict(11))
print("Survival probablity for t=840: ", kmf.predict(840))

print(kmf.predict([0,5,11,840]))
Survival probablity for t=0: 1.0
Survival probablity for t=5: 0.9956140350877193
Survival probablity for t=11: 0.9824561403508766
Survival probablity for t=840: 0.06712742409441387
0 1.000000
5 0.995614
11 0.982456
840 0.067127
Name: KM_estimate, dtype: float64

生存関数

# Get survial full list
print(kmf.survival_function_)

KM_estimate
timeline
0.0 1.000000
5.0 0.995614
11.0 0.982456
12.0 0.978070
13.0 0.969298
… …
840.0 0.067127
883.0 0.050346
965.0 0.050346
1010.0 0.050346
1022.0 0.050346

[187 rows x 1 columns]

生存確率図

# Plot the survival graph
kmf.plot()
plt.title("Kaplan-Meier")
plt.xlabel("Number o days")
plt.ylabel("Probablity of survival")
plt.show()

生存期間の中央値

# Get survial time median
survival_time_median = kmf.median_survival_time_
print(" The median survial time: ", survival_time_median)

The median survival time: 310.0

生存関数と信頼区間

# Plot survival function with confidence interval
survival_confidence_interval = kmf.confidence_interval_survival_function_
plt.plot(survival_confidence_interval['KM_estimate_lower_0.95'], label="Lower")
plt.plot(survival_confidence_interval['KM_estimate_upper_0.95'], label="Upper")
plt.title("Survival Function with confidence interval")
plt.xlabel("Number of days")
plt.ylabel("Survial Probablity")
plt.legend()
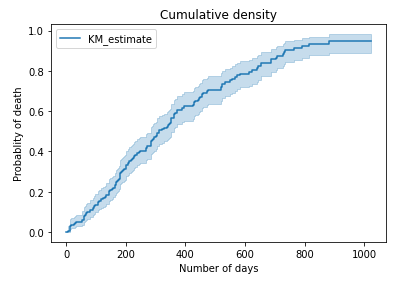
plt.show()

累積生存

# Cumulative survival
cumu_surv = kmf.cumulative_density_
# Plot cumulative density
kmf.plot_cumulative_density()
plt.title("Cumulative density")
plt.xlabel("Number of days")
plt.ylabel("Probablity of death")
plt.show()

生存期間の中央値

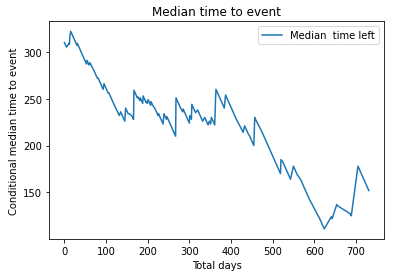
# Median time left for event
median_time_to_event = kmf.conditional_time_to_event_
plt.plot(median_time_to_event, label = "Median time left")
plt.title("Median time to event")
plt.xlabel("Total days")
plt.ylabel("Conditional median time to event")
plt.legend()
plt.show()

3.2 Kaplan-Meierの比較

男性と女性の生存期間を比較します。
男性と女性のデータを作成します。

# KM for Male and Female
kmf_m = KaplanMeierFitter()
kmf_f = KaplanMeierFitter()
Male = df.query("sex == 1")
Female = df.query("sex == 2")
kmf_m.fit(durations=Male.time, event_observed=Male.dead, label="Male")
kmf_f.fit(durations=Female.time, event_observed=Female.dead, label="Female")

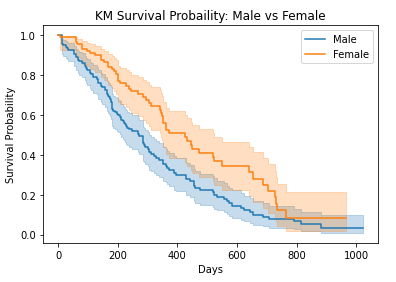
生存関数の比較

# Plot survival function
kmf_m.plot()
kmf_f.plot()
plt.title("KM Survival Probaility: Male vs Female")
plt.xlabel("Days")
plt.ylabel("Survival Probability")
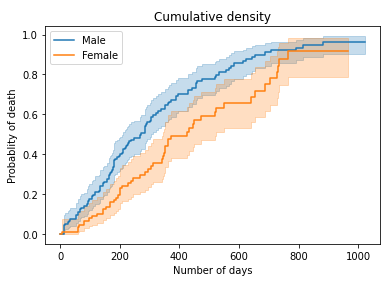
plt.show()

累積生存の比較

# Plot cumulative density
kmf_m.plot_cumulative_density()
kmf_f.plot_cumulative_density()
plt.title("Cumulative density")
plt.xlabel("Number of days")
plt.ylabel("Probablity of death")
plt.show()

3.3 ログランク検定（Log-rank）

ログランク検定は、2つのサンプルの仮説検定の生存分布です。
0と1の間のp値は、統計的有意性を示します。 p値が小さいほど、調査対象のグループ間の統計的差異が大きくなります。
0.05未満のP値は、比較したグループ間に有意差があることです。

from lifelines.statistics import logrank_test

time_m = Male.time
event_m = Male.dead

time_f = Female.time
event_f = Female.dead

results = logrank_test(time_m, time_f, event_m, event_f)
results.print_summary()
print("P-value: ", results.p_value)

P値は0.05未満になるので、男性と女性の生存関数は有意的に異なります。

担当者：KW
バンコクのタイ出身　データサイエンティスト
製造、マーケティング、財務、AI研究などの様々な業界にPSI生産管理、在庫予測・最適化分析、顧客ロイヤルティ分析、センチメント分析、SaaS、PaaS、IaaS、AI at the Edge の環境構築などのスペシャリスト

目次

1. 生存分析の概要

2. 使用事例

3. 実験

3.1 Kaplan-Meier

3.2 Kaplan-Meierの比較