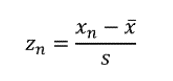目次
1. 外れ値とは
2. 外れ値と異常値の違い
3. 1次元の外れ値検定
3.1 四分位範囲(IQR)
3.2 zスコア
1.外れ値とは
外れ値とは、統計において他の値と比べて極端に大きな値かもしくは極端に小さな値のことを指します。
2. 外れ値と異常値の違い
外れ値と異常値はほぼ同じように用いられることが多いような気もしますが、基本的に異常値と外れ値は意味が違います。
異常値とは、外れ値のうち、原因(測定ミス、記録ミスなど)がわかっている値のことをいいます。
3. 1次元の外れ値検定
一概に外れ値の検出方法と言っても様々な手法があります。重要なことはデータセットに合わせた正しい手法の選択と、正しい外れ値を検出できることです。
今回は1次元のデータの外れ値検定を解説します。今回は、統計的な手法に着目し、機械学習の深層学習でのやり方は紹介していません。
1次元の外れ値検定
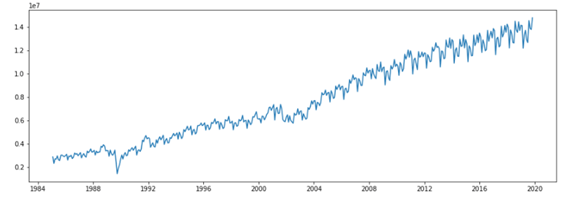
1次元のデータは1つの変数のデータです。例えば、以下の図のような1次元時系列データです。
3.1 四分位範囲(IQR)
四分位数は、データの値を小さい順に並べた時にデータを4つに分割する時の区切り値のことを指します。小さい順に第1四分位数(Q1)、第2四分位数(Q2)、第3四分位数(Q3)となり、第2四分位数はデータ全体の中央値を指します。
四分位範囲(IQR) = 第3四分位数(Q3) ー 第1四分位数(Q1)
パラメタ
– span (計算期間)
– threshold (しきい値)
メリット
– シンプル、速い
– 非正規分布データに対応できる
デメリット
– 季節性を無視する
– 線形順方向しきい値帯域
実験
サンプルデータ作成
| import numpy as np import pandas as pd import matplotlib.pyplot as plt
# 乱数を固定 rand = np.random.RandomState(seed=20)
# データを生成 date = pd.date_range(start=’2018-01-01′, end=’2020-12-31′, freq=’D’) x = np.arange(len(date)) y = 50000 \ + x ** 2 \ + np.sin(x/4) * 100000 \ + rand.randn(len(x)) * 100000 \ + rand.gamma(0.01, 1000000, len(x)) # noise
# dfに変換 df = pd.DataFrame({‘date’: date, ‘value’: y})
# Add Change point df[‘value’] = np.where((df.date >= ‘2019-01-01’) & (df.date <= ‘2019-12-31’), df[‘value’] + 800000, df[‘value’])
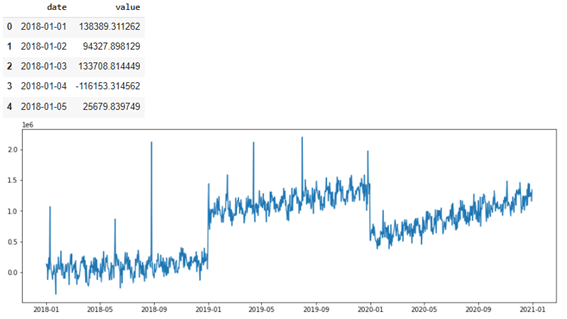
# 描画 display(df.head())
# Plot plt.plot(df.date, df.value) plt.show() |
IQRの計算と可視化
| def iqr_outlier(input_df, span=30, threshold=3): df = input_df.copy() q1 = df[‘value’].rolling(min_periods=1, window=span).quantile(0.25) q3 = df[‘value’].rolling(min_periods=1, window=span).quantile(0.75) iqr = q3 – q1 iqr_lower = q1 -(iqr * threshold) iqr_upper = q3 +(iqr * threshold) df[‘iqr’] = iqr df[‘iqr_lower’] = iqr_lower df[‘iqr_upper’] = iqr_upper df[‘iqr_outlier’] = df.value[(df.value < df.iqr_lower) | (df.value > df.iqr_upper)]
return df
outlier_df = iqr_outlier(df)
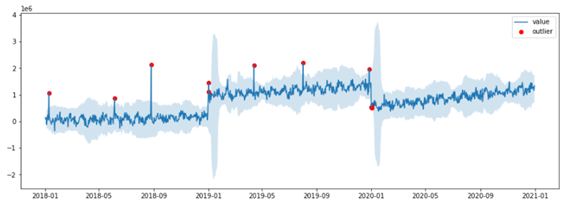
def iqr_plot(df): plt.plot(df.date, df.value, label=’value’) # Value # plt.plot(df.date, df.iqr, label=’iqr’) plt.fill_between(df.date, df.iqr_lower, df.iqr_upper, alpha=0.2) # Upper Lower plt.scatter(df.date, df.iqr_outlier, label=’outlier’, color=’r’) # Outlier plt.legend() plt.show()
iqr_plot(outlier_df) |
3.2 zスコア
zスコア(z-score)はデータを平均値を0、標準偏差を1になるように変換した値のことです。zスコアによる外れ値検出は有意水準によって決定されます。有意水準が-2と2であれば、外れ値でないデータは95.45%の中に含まれることになり、-3と3では99.73%の中に含まれることになります。
zスコアの計算:
パラメタ
– span (計算期間)
– threshold (しきい値)
メリット
– シンプル、速い
デメリット
– 非正規分布データに対応できない
– 季節性を無視する
– 初期中に外れ値を検出しにくい
実験:
| def ma_outlier(input_df, span=30, threshold=3.0): df = input_df.copy() ma_mean = df[‘value’].rolling(min_periods=1, window=span).mean() ma_std = df[‘value’].rolling(min_periods=1, window=span).std() ma_lower = ma_mean – ma_std * threshold ma_upper = ma_mean + ma_std * threshold df[‘ma_mean’] = ma_mean df[‘ma_std’] = ma_std df[‘ma_lower’] = ma_lower df[‘ma_upper’] = ma_upper df[‘ma_outlier’] = df.value[(df.value – df.ma_mean).abs() > df.ma_std * threshold]
return df
outlier_df = ma_outlier(df)
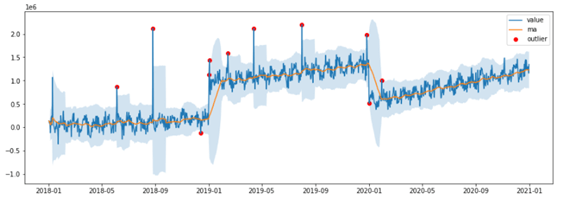
def ma_plot(df): plt.plot(df.date, df.value, label=’value’) # Value plt.plot(df.date, df.ma_mean, label=’ma’) # mean plt.fill_between(df.date, df.ma_lower, df.ma_upper, alpha=0.2) # Upper Lower plt.scatter(df.date, df.ma_outlier, label=’outlier’, color=’r’) # Outlier plt.legend() plt.show()
ma_plot(outlier_df) |
担当者:HM
香川県高松市出身 データ分析にて、博士(理学)を取得後、自動車メーカー会社にてデータ分析に関わる。その後コンサルティングファームでデータ分析プロジェクトを歴任後独立 気が付けばデータ分析プロジェクトだけで50以上担当
理化学研究所にて研究員を拝命中 応用数理学会所属