前回の記事は【ROC曲線とAUC】機械学習の評価指標を説明しました。今回の記事はマシューズ相関係数を説明します。
マシューズ相関係数とは
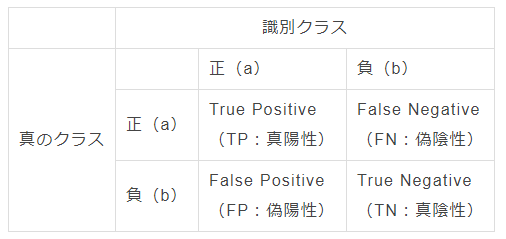
マシューズ相関係数とはMCC(Matthews Correlation Coefficient)と言われて、2値分類モデルの精度をみる指標です。真陽性と陰陰陽性と陰性を考慮し、クラスが非常に異なるサイズであっても使用できるバランスの取れた尺度と一般的にみなされます。MCCは、本質的に、- 1と+1との間の相関係数値である。 + 1の係数は完全予測を表し、0は平均ランダム予測を表し、-1は逆予測を表す。
統計は、φ係数としても知られています。 MCCは、2×2コンティンジェンシーテーブルのカイ2乗統計量に関連しています。
Matthews Correlation Coefficient
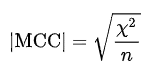
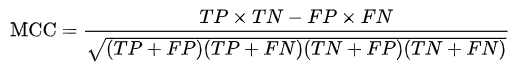
では、PythonのSklearnで作成してみましょう。
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from sklearn.metrics import matthews_corrcoef
from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score
from sklearn.metrics import confusion_matrix
# サンプルデータの生成
# 1000 samples、5(infomative) + 2(redundant) + 13(independent) = 20 feature のデータを生成
dat = make_classification(n_samples=10000, n_features=20, n_informative=5, n_redundant=2, n_classes=2, n_clusters_per_class=10,weights=[0.9, 0.1])
X = dat[0]
y = dat[1]
# 学習用とテスト用データの分割
# 80%を学習、20%をテストに利用する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
# 学習モデルの構築とパフォーマンス評価
# ロジスティック回帰
clf = LogisticRegression()
clf.fit(X_train, y_train)
print (roc_auc_score(y_test, clf.predict_proba(X_test)[:,1]))
0.6502001416552198
matthews_corrcoef(y_test, clf.predict(X_test))
0.10110987216282583
accuracy_score(y_test, clf.predict(X_test))
0.897
f1_score(y_test, clf.predict(X_test))
0.037383177570093455
confusion_matrix(y_test, clf.predict(X_test))
array([[1790, 2],
[ 204, 4]], dtype=int64)
# 今度はわざとモデルを少ない方のみを全て当てるモデルにする。
# ロジスティック回帰
clf = LogisticRegression(class_weight={0:1, 1:20000})
clf.fit(X_train, y_train)
print (roc_auc_score(y_test, clf.predict_proba(X_test)[:,1]))
0.595885992853147
matthews_corrcoef(y_test, clf.predict(X_test))
0.0
accuracy_score(y_test, clf.predict(X_test))
0.097
f1_score(y_test, clf.predict(X_test))
0.17684594348222427
confusion_matrix(y_test, clf.predict(X_test))
array([[ 0, 1806],
[ 0, 194]], dtype=int64)
