目次
1. ポワソン回帰
2. カウントベースのデータ(count data)
3. scikit-learnでのポワソン回帰
4. 実験
_4.1 環境構築
_4.2 データロード・加工
_4.3 ポワソン回帰
_4.4 線形回帰
_4.5 モデル評価
1. ポワソン回帰
ポアソン回帰(Poisson regression )は、カウントデータと分割表をモデル化するために使用される回帰分析の一般化線形モデル形式です。 ポアソン回帰は、応答変数Yがポアソン分布を持っていることを仮定して分析していきます。
ポアソン回帰モデルは、特に分割表のモデル化に使用される場合、対数線形モデル(log-linear model)といいます。
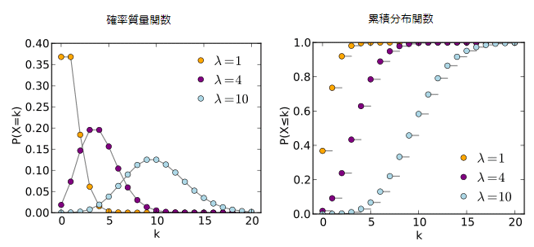
ポアソン分布(Poisson distribution)
ポアソン分布(Poisson distribution)は所与の時間内での生起回数の確率を示し、指数分布は生起期間の確率を表示します。横軸は確率変数値 k で、確率質量関数は k が 0 以上の整数のみで定義されます。整数値以外では分布関数は平らになります。
2. カウントベースのデータ(count data)
カウントベースのデータはある現象が一定時間内に起こった回数を数え上げたデータのことです。カウントベースのデータの例:
1時間に交差点を通過する車両の数、
1か月に診療所を訪れる人の数
1か月に発見された地球のような惑星の数。
カウントベースのデータの特所:
1. 整数データ:データは非負の整数で構成されます:[0…∞]
2. 偏った分布:データには、ほんの数個の値に対して多数のデータポイントが含まれている可能性があるため、度数分布がかなり歪んでいます。
3. スパース性:データはまれなイベントの発生を反映している可能性があります。
4. 発生率:モデルを作成するために、そのようなデータの生成を駆動するイベントλの特定の発生率があると想定できます。 イベントレートは時間の経過とともに変動する可能性があります。
3. scikit-learnでのポワソン回帰
sklearn.linear_model.PoissonRegressor
alphafloat, default=1
ペナルティ項を乗算し、正則化の強さを決定する定数。
fit_interceptbool, default=True
定数の設定
max_iterint, default=100
ソルバーの最大反復回数
tolfloat, default=1e-4
停止基準の設定
warm_startbool, default=False
Trueに設定されている場合は、前の呼び出しのソリューションを再利用して、coef_およびintercept_の初期の設定します。
verboseint, default=0
bfgsソルバーの場合、verboseを任意の正の数に設定して詳細度を設定します。
4. 実験
環境:Google Colab
データセット:Bicycle Counts for Brooklyn Bridgeブルックリン橋で毎月実施される自転車カウントの1日あたりの合計
https://data.cityofnewyork.us/Transportation/Bicycle-Counts-for-East-River-Bridges/gua4-p9wg
ライブラリ:scikit-learn
アルゴリズム:ポワソン回帰 vs 線形回帰
4.1 環境構築
パッケージをインストールします。
| !pip install –upgrade scikit-learn |
ライブラリインポート
| import urllib from urllib import request import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.linear_model import PoissonRegressor from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
seed = 111 np.random.seed(seed) |
4.2 データロード・加工
データセットをダウンロードします。
| # Download file url = “https://gist.github.com/sachinsdate/c17931a3f000492c1c42cf78bf4ce9fe/raw/7a5131d3f02575668b3c7e8c146b6a285acd2cd7/nyc_bb_bicyclist_counts.csv” save_path = ‘data.csv’ urllib.request.urlretrieve(url, save_path) |
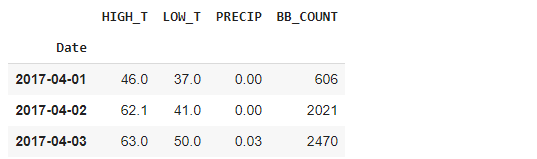
データフレーム作成
| # Create a pandas DataFrame. df = pd.read_csv(‘data.csv’, header=0, infer_datetime_format=True, parse_dates=[0], index_col=[0]) df.head(3) |
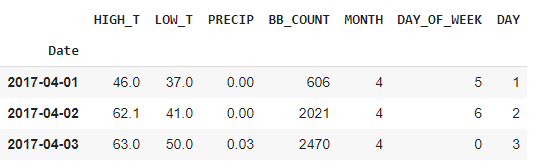
特徴量作成
| # Add a few derived regression variables. ds = df.index.to_series() df[‘MONTH’] = ds.dt.month df[‘DAY_OF_WEEK’] = ds.dt.dayofweek df[‘DAY’] = ds.dt.day df.head(3) |
学習データ・テストデータ
| # train and test split mask = np.random.rand(len(df)) < 0.8 df_train = df[mask] df_test = df[~mask] X_train = df_train.drop([‘BB_COUNT’], axis=1) y_train = df_train[“BB_COUNT”] X_test = df_test.drop([‘BB_COUNT’], axis=1) y_test = df_test[“BB_COUNT”]
print(‘Training data set length=’+str(len(df_train))) print(‘Testing data set length=’+str(len(df_test))) |
Training data set length=162
Testing data set length=52
4.3 ポワソン回帰
ポワソン回帰で学習します。
| # PoissonRegressor pr = PoissonRegressor() pr.fit(X_train, y_train) y_pr_predict = pr.predict(X_test) |
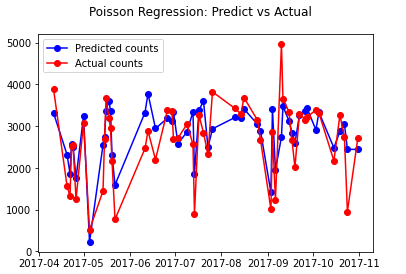
予測値と実績値を可視化します。
| # Poisson Regression: Predict vs Actual fig = plt.figure() fig.suptitle(‘Poisson Regression: Predict vs Actual’) predicted, = plt.plot(X_test.index, y_pr_predict, ‘bo-‘, label=’Predicted counts’) actual, = plt.plot(X_test.index, y_test, ‘ro-‘, label=’Actual counts’) plt.legend(handles=[predicted, actual]) plt.show() |
4.4 線形回帰
線形回帰のモデル学習します。
| # LinearRegression
lr = LinearRegression() lr.fit(X_train, y_train) y_lr_predict = lr.predict(X_test) |
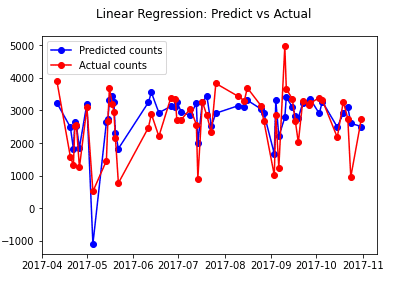
予測値と実績値を可視化します。
0以下の予測値があります。
| # Plot Linear Regression: Predict vs Actual fig = plt.figure() fig.suptitle(‘Linear Regression: Predict vs Actual’) predicted, = plt.plot(X_test.index, y_lr_predict, ‘bo-‘, label=’Predicted counts’) actual, = plt.plot(X_test.index, y_test, ‘ro-‘, label=’Actual counts’) plt.legend(handles=[predicted, actual]) plt.show() |
4.5 モデル評価
ポワソン回帰は線形回帰より良い評価値になったことがわかります。
| # Model Evaluation evaluation = pd.DataFrame() evaluation.loc[‘Poisson Regression’, ‘r2’] = r2_score(y_test, y_pr_predict) evaluation.loc[‘Poisson Regression’, ‘mse’] = mean_squared_error(y_test, y_pr_predict) evaluation.loc[‘Linear Regression’, ‘r2’] = r2_score(y_test, y_lr_predict) evaluation.loc[‘Linear Regression’, ‘mse’] = mean_squared_error(y_test, y_lr_predict) evaluation |
担当者:HM
香川県高松市出身 データ分析にて、博士(理学)を取得後、自動車メーカー会社にてデータ分析に関わる。その後コンサルティングファームでデータ分析プロジェクトを歴任後独立 気が付けばデータ分析プロジェクトだけで50以上担当
理化学研究所にて研究員を拝命中 応用数理学会所属