今回の記事はグラフィカルラッソで変数関係の可視化を説明します。
グラフィカルラッソとは
グラフィカルラッソはガウシアングラフィカルモデルに従う、確率変数ベクトルがあった時、変数間の関係を指定し、グラフ化する手法です。回帰問題を以前取扱いましたが、回帰の分析が中で行われています
sklearnからBostonデータセットの各変数間の関係をグラフ化します。
下記はボストンの物件の価格にその物件の人口統計に関する情報です。
sklearnからBostonデータセットの各変数間の関係をグラフ化します。
下記はボストンの物件の価格にその物件の人口統計に関する情報です。
CRIM | 人口 1 人当たりの犯罪発生数 (人口単位) |
ZN | 25,000 平方フィート以上の住居区画の占める割合 |
INDUS | 非小売業の土地面積の割合 (人口単位) |
CHAS | チャールズ川沿いかどうか(1:Yes、0:No) |
NOX | 窒素酸化物の濃度(pphm単位) |
RM | 住居の平均部屋数 |
AGE | 1940 年より前に建てられた物件の割合 |
DIS | 5 つのボストン市の雇用施設からの距離 (重み付け済) |
RAD | 環状高速道路へのアクセスしやすさ |
TAX | $10,000 ドルあたりの不動産税率の総計 |
PTRATIO | 町毎の児童と教師の比率 (人口単位) |
B | アフリカ系アメリカ人居住者の割合(人口単位) |
LSTAT | 給与の低い職業に従事する人口の割合 (%) |
import pydot
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
import sklearn.datasets
from sklearn.covariance import GraphLasso
import scipy as sp
dataset = sklearn.datasets.load_boston()
X=dataset.data
feature_names=dataset.feature_names
X.shape
feature_names
(506, 13)
array([‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’, ‘DIS’, ‘RAD’,
‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’], dtype='<U7′)
def Graphical_Lasso(X, alpha, disp_heatmap=True):
#データの正規化(必須)
X=sp.stats.zscore(X,axis=0)
#GraphLasso
model = GraphLasso(alpha=alpha,verbose=True)
model.fit(X)
cov=np.cov(X.T) #計算による分散共分散行列(転置を取るかはデータの向きによる)
cov_ = model.covariance_ #スパース化した分散共分散行列
pre_ = model.precision_ #スパース化した分散共分散行列の逆行列
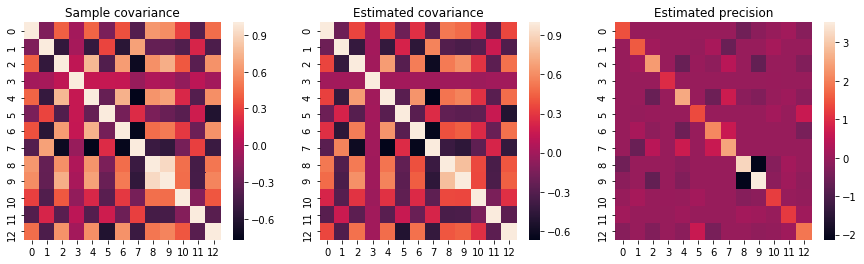
#分散共分散行列のヒートマップによる表示
if disp_heatmap==True:
f, axes = plt.subplots(1, 3, figsize=(15, 4))
axes[0].set_title(‘Sample covariance’)
axes[1].set_title(‘Estimated covariance’)
axes[2].set_title(‘Estimated precision’)
sns.heatmap(cov, ax=axes[0])
sns.heatmap(cov_, ax=axes[1])
sns.heatmap(pre_, ax=axes[2])
return model
dataset = sklearn.datasets.load_boston()
X=dataset.data
feature_names=dataset.feature_names
X.shape
feature_names
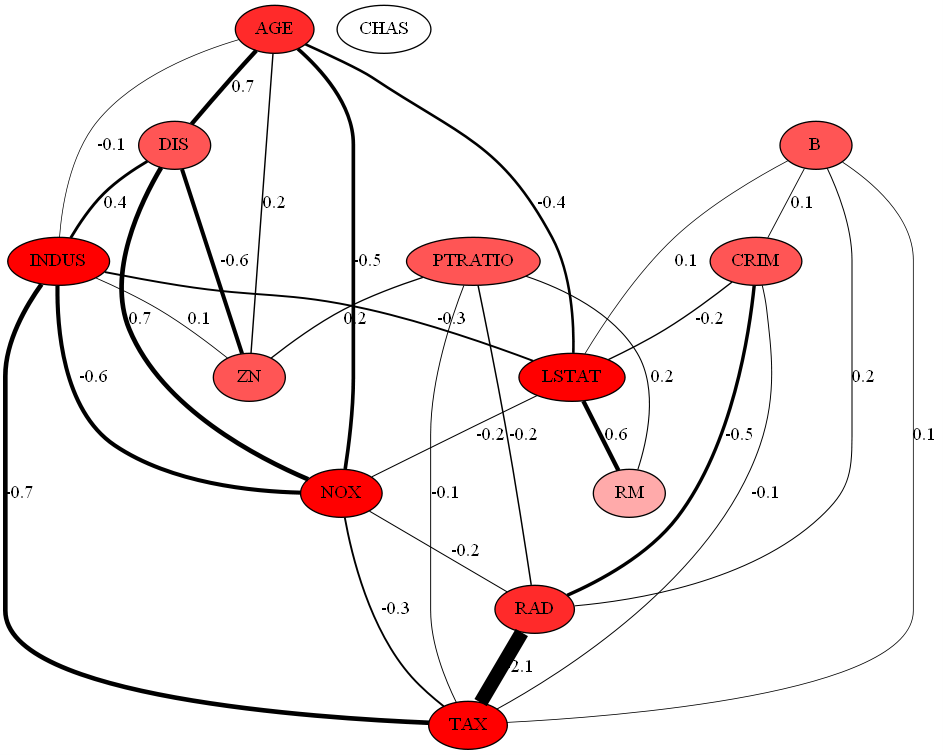
def Disp_Gaussian_Graphical_Model(model,feature_names):
pre_ = model.precision_ #スパース化した分散共分散行列の逆行列
#グラフ表示のために対角成分は0にする
pre_zero=pre_–np.diag(np.diag(pre_))
#分散共分散行列の逆行列(≒隣接行列)からグラフを生成する
g = pydot.Dot(graph_type=‘graph’)
df = pd.DataFrame(index=feature_names.tolist(),
columns=feature_names.tolist(),
data=pre_zero.tolist())
#ノードを追加
for c in df.columns:
node = pydot.Node(c)
g.add_node(node)
#エッジを追加
for i in df.index:
for c in df.columns:
if c>=i:
#エッジの絶対値が0.1より大きいときに表示(ここは好みによる)
if abs(df.loc[i, c]) > 0.1:
edge = pydot.Edge(g.get_node(i)[0], g.get_node(c)[0],
penwidth=5*abs(df.loc[i, c]))
edge.set_label(‘{:.1f}’.format(df.loc[i, c]))
g.add_edge(edge)
#結合数によって色を変える
nodeList = g.get_node_list()
num_edges=np.sum(abs(pre_zero) > 0.1, axis=0)
max_num_edges=max(np.amax(num_edges),1)
for i in range(len(df.index)):
node = nodeList[i]
# H S Vの順 Sを変更
color=str(0)+” “+str(num_edges[i]/max_num_edges)+” “+str(1)
node.set_color(“black”) #nodeの輪郭の色
node.set_fillcolor(color) #nodeの中身の色
node.set_style(‘filled’)
# グラフを出力
#g.write_png(‘LassoEstimatedGGM.png’, prog=’neato’)
g.write_png(‘LassoEstimatedGGM.png’)
def Compute_extended_BIC(model,n,p,cov,gamma):
omega = model.precision_
E=(np.sum(np.sum(omega != 0, axis=0))–p)*0.5
#尤度
MLE=n*(np.log(np.linalg.det(omega))–np.trace(np.dot(cov,omega)))
EBIC=-MLE+E*np.log(n)+4*E*gamma*np.log(p)
return EBIC
def main():
#Dataをインポート
dataset = sklearn.datasets.load_boston()
X=dataset.data
feature_names=dataset.feature_names
cov=np.cov(X.T) #標本分散共分散行列
#普通はn(サンプル数)>p(変数の数)なので
n=max(X.shape[0],X.shape[1]) #サンプル数
p=min(X.shape[0],X.shape[1]) #変数の数(ノード数)
#Graphical Lassoの実行
alpha=0.1 #L1正則化パラメータ
model=Graphical_Lasso(X, alpha)
#BIC, EBICの計算
BIC=Compute_extended_BIC(model,n,p,cov,0)
print(“BIC :”+str(BIC)+” alpha :”+str(alpha))
EBIC=Compute_extended_BIC(model,n,p,cov,0.5)
print(“EBIC :”+str(EBIC)+” alpha :”+str(alpha))
#グラフ化
Disp_Gaussian_Graphical_Model(model,feature_names)
if __name__ == ‘__main__’:
main()
[graphical_lasso] Iteration 0, cost 5.54e+01, dual gap 2.522e-01
[graphical_lasso] Iteration 1, cost 5.53e+01, dual gap -2.751e-02
[graphical_lasso] Iteration 2, cost 5.53e+01, dual gap -4.195e-03
[graphical_lasso] Iteration 3, cost 5.53e+01, dual gap -1.124e-03
[graphical_lasso] Iteration 4, cost 5.53e+01, dual gap -5.151e-04
[graphical_lasso] Iteration 5, cost 5.53e+01, dual gap -2.781e-04
[graphical_lasso] Iteration 6, cost 5.53e+01, dual gap -1.689e-04
[graphical_lasso] Iteration 7, cost 5.53e+01, dual gap -1.890e-04
[graphical_lasso] Iteration 8, cost 5.53e+01, dual gap -1.708e-04
[graphical_lasso] Iteration 9, cost 5.53e+01, dual gap -1.534e-04
[graphical_lasso] Iteration 10, cost 5.53e+01, dual gap -1.371e-04
[graphical_lasso] Iteration 11, cost 5.53e+01, dual gap -1.180e-04
[graphical_lasso] Iteration 12, cost 5.53e+01, dual gap -9.733e-05
BIC :52304376.89868173 alpha :0.1
EBIC :52304561.57503547 alpha :0.1